Elipse
Una elipse generalmente parece un círculo aplastado :
“F” es un enfoque , “G” es un enfoque ,
y juntos se llaman focos .
(pronunciado “fo-suspiro”)

La distancia total de F a P a G permanece igual
En otras palabras, siempre viajamos la misma distancia cuando vamos desde:
- punto “F” a
- a cualquier punto de la elipse
- y luego al punto “G”
Puedes dibujarlo tú mismo
Coloca dos pines en un tablero y luego …

poner un lazo de cuerda alrededor de ellos,

inserte un lápiz en el bucle,

estira la cuerda para que forme un triángulo,

y dibuja una curva.
Es una elipse!
Funciona porque la cuerda fuerza naturalmente la misma distancia desde pin-to-pencil-to-other-pin .
Un círculo es una elipse

De hecho, un círculo es una elipse, donde ambos focos están en el mismo punto (el centro).
En otras palabras, un círculo es un “caso especial” de una elipse. Regla de las elipses!
Definición
Una elipse es el conjunto de todos los puntos en un plano cuya distancia desde dos puntos fijos F y G se suman a una constante.
Ejes mayores y menores
El Eje principal es el diámetro más largo. Va desde un lado de la elipse, a través del centro, hacia el otro lado, en la parte más ancha de la elipse. Y el Eje menor es el diámetro más corto (en la parte más estrecha de la elipse).
El Eje Semi-mayor es la mitad del Eje Mayor, y el Eje Semi-menor es la mitad del Eje Menor.
Eje mayor igual a f + g

¿Recuerdas desde arriba cómo la distancia “f + g” se mantiene igual para una elipse?
Bueno, f + g es igual a la longitud del eje mayor .
¿Puedes pensar por qué? (Intente mover el punto P en la parte superior).
Cálculos
¡El área es fácil, el perímetro no lo es!
Área

El área de una elipse es:
π × a × b
donde a es la longitud del eje semi-mayor, y b es la longitud del eje semi-menor.
Tenga cuidado: a y b están desde el centro hacia afuera (no del todo).
(Nota: para un círculo, a y b son iguales al radio, y obtienes π × r × r = [ 19459042] π r 2 , ¡eso es correcto!)
Aproximación perimetral
Más bien extrañamente, el perímetro de una elipse es muy difícil de calcular , así que creé una página especial para el tema: leer Perímetro de una elipse para más detalles.
Pero una aproximación simple que está dentro del 5% del valor verdadero (siempre que a no sea más de 3 veces más que b ) es como sigue:
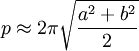
Recuerde, ¡esto es solo una aproximación aproximada! (Es por eso que el “signo igual” es ondulado).
Tangente
Una línea tangente solo toca una curva en un punto, sin cortarla.
Aquí hay una tangente a una elipse:
Aquí hay algo interesante: ¡la línea tangente tiene ángulos iguales con las dos líneas que van a cada foco! Intenta unir los dos puntos de enfoque (para que la elipse sea un círculo) … ¿qué notas?
Reflexión
La luz o el sonido que comienzan en un punto de enfoque se reflejan en el otro punto de enfoque (porque el ángulo de entrada coincide con el ángulo de salida):

Juega con un simple modelo de computadora de reflexión dentro de una elipse .
Excentricidad

La excentricidad es una medida de cuán “redondeada” es la elipse.
La fórmula (usando ejes semi-mayor y semi-menor) es:
√ (a 2 −b 2 ) a
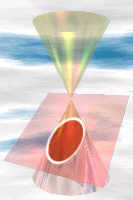
Sección de un cono
También puede obtener una elipse cuando corta a través de un cono (pero no una rebanada demasiado empinada, o obtiene una parábola o hipérbola ).
De hecho, la elipse es una sección cónica (una sección de un cono) con una excentricidad entre 0 y 1.

Ecuación
Al colocar una elipse en un gráfico x-y (con su eje mayor en el eje xy eje menor en el eje y), la ecuación de la curva es:
x 2 a 2 + y 2 [ 19459045] b 2 = 1
(similar a la ecuación de la hipérbola : x 2 / a 2 – y 2 / b [ 19459044] 2 = 1 , excepto por un “+” en lugar de un “-“)
O podemos “ecuaciones paramétricas”, donde tenemos otra variable “t” y calculamos x e y a partir de ella, así:
- x = a cos (t)
- y = b sin (t)
(Solo imagine que “t” va de 0 ° a 360 °, ¿qué valores de x e y obtendríamos?)
