Introducción al álgebra – Multiplicación
Lea Introducción al álgebra primero
Un rompecabezas
¿Cuál es el número faltante?
|
|
× | 4 | = | 8 |
La respuesta es 2, ¿verdad? Porque 2 × 4 = 8 .
Bueno, en Álgebra no usamos cuadros en blanco, usamos
una carta . Entonces podríamos escribir:
| x | × | 4 | = | 8 |
Pero el “ x ” se parece al “ × ” … eso puede ser muy confuso … así que en Álgebra no usamos el símbolo de multiplicación ( × ) entre números
y letras:
Ponemos el número al lado de la letra para significar multiplicar :
| 4 x | = | 8 |
En inglés decimos “cuatro x es igual a ocho” , lo que significa que 4 x son 8.
Y la respuesta está escrita:
| x | = | 2 |
Cómo resolver
En lugar de decir “ obviamente x = 2″, utilice este enfoque ordenado paso a paso:
- Calcula qué eliminar para obtener “x = …”
- Eliminarlo haciendo lo contrario
- Haz eso a ambos lados
¿Y qué es lo contrario de multiplicar? ¡Dividiendo!
Eche un vistazo a este ejemplo:
a
quitar
el “4”
Para eliminarlo, haz
lo contrario , en
este caso se divide por 4
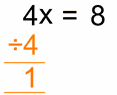
Hazlo a
ambos lados
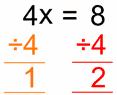
Que es …
Resuelto!
¿Por qué dividimos por 4 en ambos lados?
Debido a la necesidad de equilibrio …
 |
| En equilibrio |
| Dividir a la izquierda entre 4 |
 |
| ¡Fuera de balance! |
| Dividir a la derecha entre 4 también |
 |
| En equilibrio otra vez |
Solo recuerda …
| Para mantener el equilibrio, lo que hacemos a a un lado del “=” ¡también deberíamos hacerlo al otro lado ! |
Otro rompecabezas
Resuelve este:
| x | / | 3 | = | 5 |
Lo que queremos es una respuesta como “x = …”, pero la división entre 3 está en el camino de eso.
Si multiplicamos por 3 podemos cancelar la división por 3 (porque 3/3 = 1)
Pruébalo tú mismo
Ahora practica en esta Hoja de trabajo de multiplicación de álgebra y luego verifica tus respuestas en la página siguiente. ¡Intenta usar los pasos que te hemos mostrado aquí, en lugar de solo adivinar!
Ejemplo más complicado
¿Cómo resolvemos esto?
| x | / | 3 | + | 2 | = | 5 |
Puede parecer difícil, pero no si lo resolvemos en etapas .
Primero eliminemos el “+2”:
Ahora, deshazte del “/ 3”:
Cuando tienes más experiencia:
Cuando tengas más experiencia, puedes resolverlo así:
O más rápido así:
Ejemplo del mundo real

Ejemplo: Sam compró 3 cajas de bombones en línea.
El franqueo fue de $ 9 y el costo total fue de $ 45.
¿Cuánto fue cada caja?
Usemos x para el precio de cada caja.
3 veces x más $ 9 es $ 45:
3x + 9 = 45
¡A resolver!
Entonces cada caja era $ 12
Avanzado: también podemos hacer primero “dividir por 3” (pero debemos hacerlo en todos los términos):
La misma respuesta.
Pruébalo tú mismo
Ahora practica en esta Álgebra (Dos pasos para resolver) Hoja de trabajo y luego verifica tus respuestas en la página siguiente. ¡Intenta usar los pasos que te hemos mostrado aquí, en lugar de solo adivinar!
