
Álgebra – Sustitución
“Sustituto” significa poner en el lugar de otro.
Sustitución
En álgebra “sustitución” significa poner números donde están las letras:
| |
Cuando tenemos: |
|
|||||
| |
Y sabemos que x = 6 … | ||||||
| |
… entonces podemos “sustituir” 6 por x : |
|
Ejemplo: cuando x = 2, ¿cuál es 10 / x + 4 ?
Pon “2” donde “x” es:
10 / 2 + 4 = 5 + 4 = 9
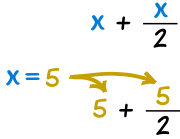
Ejemplo: cuando x = 5, ¿cuál es x + x / 2 ?
Pon “5” donde “x” es:
5 + 5 / 2 = 5 + 2.5 = 7.5
Ejemplo: Si x = 3 e y = 4, entonces ¿cuál es x 2 + xy ?
Pon “3” donde “x” es, y “4” donde “y” es:
3 2 + 3 × 4 = 3 × 3 + 12 = 21
Ejemplo: Si x = 3 (pero no sabemos “y”), entonces ¿cuál es x 2 + xy ?
Pon “3” donde “x” es:
3 2 + 3 y = 9 + 3y
(hasta aquí podemos llegar)
Como mostró el último ejemplo, no siempre podemos obtener un número para una respuesta, a veces solo una fórmula más simple.
Números negativos
Cuando sustituyas números negativos, coloca () alrededor de ellos para obtener los cálculos correctos.
Ejemplo: Si x = −2 , entonces ¿cuál es 1 – x + x 2 ?
Pon “(−2)” donde “x” es:
1 – (−2) + [ 19459020] (−2) 2 = 1 + 2 + 4 = 7
En ese último ejemplo:
- el – (−2) se convirtió en +2
- el (−2) 2 se convirtió en +4
debido a estas reglas especiales:
| Regla | Agregando o Restando |
Multiplicar o División |
||
|---|---|---|---|---|
| |
Dos signos similares se convierten en un signo positivo | 3 + (+ 2) = 3 + 2 = 5 | 3 × 2 = 6 | |
| 6 – (- 3) = 6 + 3 = 9 | (−3) × (−2) = 6 | |||
| |
Dos signos diferentes se convierten en un signo negativo | 7 + (- 2) = 7 – 2 = 5 | 3 × (−2) = −6 | |
| 8 – (+ 2) = 8 – 2 = 6 | (−3) × 2 = −6 |
