Simplificando raíces cuadradas
Para simplificar una raíz cuadrada: haga que el número dentro de la raíz cuadrada sea lo más pequeño posible (pero sigue siendo un número entero ):
Ejemplo: √12 es más simple que 2√3
Obtenga su calculadora y verifique si lo desea: ¡ambos tienen el mismo valor!
Aquí está la regla: cuando ayb no son negativos
Y aquí está cómo usarlo:
Ejemplo: simplificar √12
12 es 4 veces 3:
Usa la regla:
Y la raíz cuadrada de 4 es 2:
Entonces √12 es más simple que 2√3
Otro ejemplo:
Ejemplo: simplificar √8
(Porque la raíz cuadrada de 4 es 2)
Y otro:
Ejemplo: simplificar √18
√18 = √ (9 × 2) = √9 × √2 = 3√2
A menudo ayuda factorizar los números (en números primos es lo mejor):
Ejemplo: simplificar √6 × √15
Primero podemos combinar los dos números:
Luego los factorizamos:
Luego vemos dos 3s, y decidimos “sacarlos”:
Fracciones
Hay una regla similar para las fracciones:
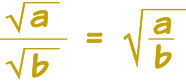
Ejemplo: simplificar √30 / √10
Primero podemos combinar los dos números:
Luego simplifica:
Algunos ejemplos más difíciles
Ejemplo: simplificar √20 × √5 √2
Vea si puede seguir los pasos:
Ejemplo: simplificar 2√12 + 9√3
Primero simplifica 2√12:
Ahora ambos términos tienen √3, podemos agregarlos:
Surds
Nota: una raíz que no podemos simplificar aún más se llama Surd . Entonces √3 es una sorpresa. Pero √4 = 2 no es una sorpresa.
