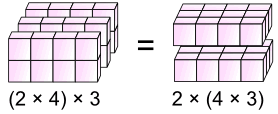Leyes conmutativas, asociativas y distributivas
¡Guau! ¡Qué bocado de palabras! Pero las ideas son simples.
Leyes conmutativas
Las “Leyes conmutativas” dicen que podemos intercambiar números y aún así obtener la misma respuesta …
… cuando agregamos :
a + b = b + a
Ejemplo:
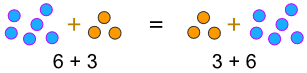
… o cuando multiplicamos :
a × b = b × a
Ejemplo:
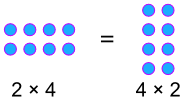
¡Porcentajes conmutativos!
Porque a × b = b × a también es cierto que a% de b = b% de a [ 19459006]
Ejemplo: 8% de 50 = 50% de 8, que es 4

¿Por qué “conmutativo ” …?
Porque los números pueden viajar de un lado a otro como un viajero .
Leyes asociativas
Las “Leyes asociativas” dicen que no importa cómo agrupamos los números (es decir, qué calculamos primero) …
… cuando agregamos :
(a + b) + c = a + (b + c)
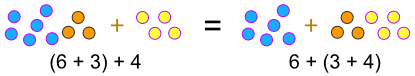
… o cuando multiplicamos :
(a × b) × c = a × (b × c)
Ejemplos:
| Esto: | (2 + 4) + 5 = 6 + 5 = 11 |
| Tiene la misma respuesta que esta: | 2 + (4 + 5) = 2 + 9 = 11 |
| Esto: | (3 × 4) × 5 = 12 × 5 = 60 |
| Tiene la misma respuesta que esta: | 3 × (4 × 5) = 3 × 20 = 60 |
Usos:
A veces es más fácil agregar o multiplicar en un orden diferente:
¿Qué es 19 + 36 + 4?
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
O para reorganizar un poco:
¿Qué es 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
Ley distributiva
La “Ley Distributiva” es la MEJOR de todas, pero necesita una atención cuidadosa.
Esto es lo que nos permite hacer:
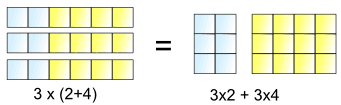
3 lotes de (2 + 4) es lo mismo que 3 lotes de 2 más 3 lotes de 4
Entonces, 3 × se puede “distribuir” en 2 + 4 , en 3 × 2 y 3 × 4 [19459012 ]
Y lo escribimos así:
a × (b + c) = a × b + a × c
Pruebe los cálculos usted mismo:
- 3 × ( 2 + 4 ) = 3 × 6 = 18
- 3 × 2 + 3 × 4 = 6 + 12 = 18
De cualquier manera se obtiene la misma respuesta.
En inglés podemos decir:
Obtenemos la misma respuesta cuando:
- multiplica un número por un grupo de números sumados o
- multiplica cada por separado y luego agrega
Usos:
A veces es más fácil romper una multiplicación difícil:
Ejemplo: ¿Qué es 6 × 204?
6 × 204 = 6 × 200 + 6 × 4
= 1.200 + 24
= 1,224
O para combinar:
Ejemplo: ¿Qué es 16 × 6 + 16 × 4?
16 × 6 + 16 × 4 = 16 × (6 + 4)
= 16 × 10
= 160
Podemos usarlo también en resta:
Ejemplo: 26 × 3 – 24 × 3
= 2 × 3
= 6
También podríamos usarlo para una larga lista de adiciones:
Ejemplo: 6 × 7 + 2 × 7 + 3 × 7 + 5 × 7 + 4 × 7
6 × 7 + 2 × 7 + 3 × 7 + 5 × 7 + 4 × 7
= (6 + 2 + 3 + 5 + 4) × 7
= 20 × 7
= 140
Y esas son las Leyes. . .
. . . pero no vayas muy lejos!
La Ley Conmutativa no funciona para la resta o división:
Ejemplo:
- 12/3 = 4 , pero
- 3/12 = ¼
La Ley asociativa no funciona para la resta o división:
Ejemplo:
- (9 – 4) – 3 = 5 – 3 = 2 , pero
- 9 – (4 – 3) = 9 – 1 = 8
La Ley Distributiva no funciona para la división:
Ejemplo:
- 24 / (4 + 8) = 24/12 = 2 , pero
- 24/4 + 24/8 = 6 + 3 = 9
Resumen
| Leyes conmutativas: | a + b = b + a a × b = b × a |
| Leyes asociativas: | (a + b) + c = a + (b + c) (a × b) × c = a × (b × c) |
| Ley distributiva: | a × (b + c) = a × b + a × c |