Proporciones
La proporción dice que dos proporciones (o fracciones) son iguales.
Ejemplo:
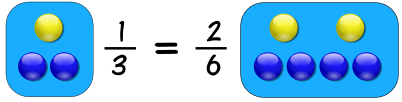
Entonces 1 de 3 es igual a 2 de 6
Las proporciones son las mismas, por lo que son proporcionales.
Ejemplo: cuerda
La longitud de una cuerda y peso son proporcionales.
Cuando 20m de cuerda pesa 1 kg , entonces:
- 40m de esa cuerda pesa 2kg
- 200m de esa cuerda pesa 10kg
- etc.
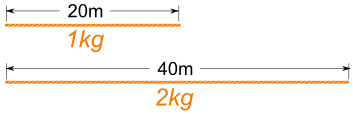
Entonces:
20
1
=
40
2
Tamaños
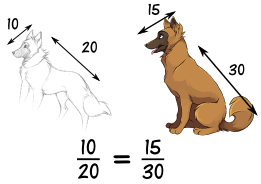
Cuando las formas están “en proporción”, sus tamaños relativos son los mismos.
|
Aquí vemos que las relaciones entre la longitud de la cabeza y la longitud del cuerpo son las mismas en ambos dibujos. Entonces son proporcionales . ¡Hacer que la cabeza sea demasiado larga o corta se vería mal! |
 |
Ejemplo: Los tamaños de papel internacionales (como A3, A4, A5, etc.) tienen todas las mismas proporciones:

Por lo tanto, cualquier obra de arte o documento puede redimensionarse para caber en cualquier hoja. Muy aseado.
Trabajando con proporciones
AHORA, ¿cómo usamos esto?
Ejemplo: quieres dibujar la cabeza del perro … ¿cuánto tiempo debe ser?
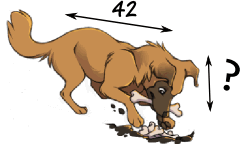
Escribamos la proporción con la ayuda de la relación 10/20 desde arriba:
?
42
=
10
20
Ahora
lo resolvemos usando un método especial:

Multiplica por las esquinas conocidas,
luego dividir por el tercer número
Y obtenemos esto:
? = (42 × 10) / 20
= 420/20
= 21
Entonces debes dibujar la cabeza 21 de largo.
Usando proporciones para resolver porcentajes
¡Un porcentaje es en realidad una proporción! Decir “25%” en realidad es decir “25 por 100”:
25% = 25 100
Podemos usar proporciones para resolver preguntas que involucran porcentajes.
El truco es poner lo que sabemos en esta forma:
Parte Entero = Porcentaje 100
Ejemplo: ¿cuál es el 25% de 160?
El porcentaje es 25, el total es 160 y queremos encontrar la “parte”:
Parte 160 = 25 100
Multiplica por las esquinas conocidas, luego divide por el tercer número:

Parte = (160 × 25) / 100
= 4000/100
= 40
Respuesta: 25% de 160 es 40.
Nota: también podríamos haber resuelto esto haciendo la división primero, así:
Parte = 160 × (25/100)
= 160 × 0.25
= 40
Cualquiera de los métodos funciona bien.
También podemos encontrar un porcentaje:
Ejemplo: ¿qué es $ 12 como porcentaje de $ 80?
Complete lo que sabemos:
$ 12 $ 80 = Porcentaje 100
Multiplica por las esquinas conocidas, luego divide por el tercer número. Esta vez las esquinas conocidas son arriba a la izquierda y abajo a la derecha:

Porcentaje = ($ 12 × 100) / $ 80
= 1200/80
= 15%
Respuesta: $ 12 es 15% de $ 80
O encuentra el conjunto:
Ejemplo: el precio de venta de un teléfono era de $ 150, que era solo el 80% del precio normal. ¿Cuál fue el precio normal?
Complete lo que sabemos:
$ 150 Entero = 80 100
Multiplica por las esquinas conocidas, luego divide por el tercer número:

Entero = ($ 150 × 100) / 80
= 15000/80
= 187,50
Respuesta: el precio normal del teléfono era $ 187.50
Usando proporciones para resolver triángulos
Podemos usar proporciones para resolver triángulos similares.
Ejemplo: ¿Qué altura tiene el árbol?
Sam intentó usar una escalera, cinta métrica, cuerdas y varias otras cosas, pero aún no pudo determinar qué tan alto era el árbol.
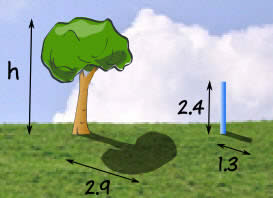
Pero Sam tiene una idea inteligente … ¡triángulos similares!
Sam mide un palo y su sombra (en metros), y también la sombra del árbol, y esto es lo que obtiene:
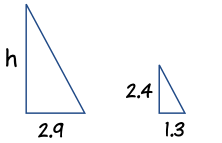
Ahora Sam hace un boceto de los triángulos y escribe la relación “Altura a longitud” para ambos triángulos:
Altura:
Longitud de sombra: h
2,9 m =
2,4 m
1,3 m
Multiplica por las esquinas conocidas, luego divide por el tercer número:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5.4 m (al 0.1 más cercano)
Respuesta: el árbol tiene 5,4 m de altura.
¡Y ni siquiera necesitaba una escalera!
La “Altura” podría haber estado en la parte inferior, siempre y cuando estuviera en la parte inferior para AMBAS proporciones, como esta:

Probemos la relación de “Longitud de sombra a Altura”:
Longitud de las sombras:
Altura:
2,9 m
h =
1,3 m
2,4 m
Multiplica por las esquinas conocidas, luego divide por el tercer número:
h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5.4 m (al 0.1 más cercano)
Es el mismo cálculo que antes.
Un ejemplo de “concreto”
¡Las proporciones pueden tener más de dos números !
Por ejemplo, el hormigón se hace mezclando cemento, arena, piedras y agua.

Una mezcla típica de cemento, arena y piedras se escribe como una proporción, como 1: 2: 6 .
Podemos multiplicar todos los valores por la misma cantidad y seguir teniendo la misma proporción.
10:20:60 es lo mismo que 1: 2: 6
Entonces, cuando usamos 10 cubos de cemento, debemos usar 20 de arena y 60 de piedras.
Ejemplo: acaba de colocar 12 cubos de piedras en una mezcladora, ¿cuánto cemento y cuánta arena debe agregar para hacer una mezcla 1: 2: 6 ?
Pongámoslo en una mesa para aclararlo:
| Cemento | Arena | Piedras | |
|---|---|---|---|
| Proporción necesaria: | 1 | 2 | 6 |
| Tienes: | 12 |
Tienes 12 cubos de piedras pero la proporción dice 6.
Eso está bien, simplemente tienes el doble de piedras que el número en la proporción … así que necesitas el doble de todo para mantener la proporción.
Aquí está la solución:
| Cemento | Arena | Piedras | |
|---|---|---|---|
| Proporción necesaria: | 1 | 2 | 6 |
| Tienes: | 2 | 4 | 12 |
Y la proporción 2: 4: 12 es la misma que 1: 2: 6 (porque muestran los mismos tamaños relativo )
Entonces la respuesta es: agregue 2 cubos de cemento y 4 cubos de arena. (También necesitará agua y mucha agitación …)
¿Por qué tienen la misma proporción? Bueno, la relación 1: 2: 6 dice tener :
- el doble de arena que cemento ( 1 : 2 : 6)
- 6 veces más piedras que cemento ( 1 : 2: 6 )
En nuestra mezcla tenemos:
- dos veces más arena que cemento ( 2 : 4 : 12)
- 6 veces más piedras que cemento ( 2 : 4: 12 )
¡Entonces debería ser lo correcto!
Eso es lo bueno de las razones. Puede hacer que las cantidades sean más grandes o más pequeñas y siempre que los tamaños relativos sean los mismos y la relación sea la misma.
