Polinomios
Un polinomio se ve así:
 |
| ejemplo de un polinomio éste tiene 3 términos |
El polinomio proviene de poli- (que significa “muchos”) y -nomial (en este caso significa “término”) … así dice “muchos términos”
Un polinomio puede tener:
| constantes (como 3 , −20 , o ½ ) |
| variables (como x y y ]) |
| exponentes (como el 2 en y 2 ), pero solo 0, 1, 2, 3, … etc. están permitidos |
que se puede combinar usando suma, resta, multiplicación y división …
… excepto …
| … no división por una variable (así que algo como 2 / x está en orden) |
Entonces:
Un polinomio puede tener constantes, variables y exponentes,
pero nunca división por una variable.
También pueden tener uno o más términos, pero no un número infinito de términos.
¿Polinomio o no?

Estos son polinomios:
- 3x
- x – 2
- −6y 2 – (
7
9
) x - 3xyz + 3xy 2 z – 0.1xz – 200y + 0.5
- 512v 5 + 99w 5
- 5
(Sí, “5” es un polinomio, se permite un término , ¡y puede ser solo una constante!)
Estos son no polinomios
- 3xy -2 no lo es, porque el exponente es “-2” (los exponentes solo pueden ser 0,1,2, …)
- 2 / (x + 2) no lo es, porque no se permite dividir por una variable
- 1 / x tampoco es
- √x no lo es, porque el exponente es “½” (ver exponentes fraccionales )
Pero estos están permitidos:
- x / 2 está permitido , porque se puede dividir por una constante
- también 3x / 8 por la misma razón
- √2 está permitido, porque es una constante (= 1.4142 … etc.)
Monomial, Binomial, Trinomial
Hay nombres especiales para polinomios con 1, 2 o 3 términos:

¿Cómo recuerdas los nombres? Piensa en ciclos!

También hay quadrinomial (4 términos) y quintinomial (5 términos),
pero esos nombres no se usan con frecuencia.
Variables
Los polinomios no pueden tener ninguna variable en absoluto
Ejemplo: 21 es un polinomio. Tiene solo un término, que es una constante.
O una variable
Ejemplo: x 4 – 2x 2 + x tiene tres términos, pero solo una variable (x)
O dos o más variables
Ejemplo: xy 4 – 5x 2 z tiene dos términos y tres variables (x, y y z)
¿Qué tienen de especial los polinomios?
Debido a la definición estricta, los polinomios son fáciles de trabajar con .
Por ejemplo, sabemos que:
- Si agrega polinomios obtendrá un polinomio
- Si multiplica polinomios obtendrá un polinomio
Entonces puedes hacer muchas adiciones y multiplicaciones, y aún así tener un polinomio como resultado.
Además, los polinomios de una variable son fáciles de graficar, ya que tienen líneas suaves y continuas.
Ejemplo: x 4 −2x 2 + x
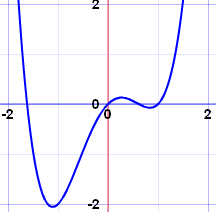 |
Mira qué lindo y |
También puede dividir polinomios (pero el resultado puede no ser un polinomio).
Grado
El grado de un polinomio con una sola variable es el mayor exponente de esa variable.
Ejemplo:
| |
El grado es 3 (el mayor exponente de x ) |
Para casos más complicados, lea Grado (de una expresión) .
Formulario estándar
El Formulario estándar para escribir un polinomio es poner los términos con el grado más alto primero.
Ejemplo: Ponga esto en forma estándar: 3 x 2 – 7 + 4 x 3 + x [ 19459029] 6
El grado más alto es 6, por lo que va primero, luego 3, 2 y luego el último constante:
x 6 + 4 x 3 + 3 x 2 – 7
Usted no tiene que usar el formulario estándar, pero ayuda.
