
Polinomios – División larga
Un polinomio se ve así:
 |
| ejemplo de un polinomio este tiene 3 términos |
División

Los polinomios a veces se pueden dividir utilizando los métodos simples que se muestran en División de polinomios .
Pero a veces es mejor usar “División larga” (un método similar a División larga para números )
Numerador y Denominador
Podemos dar un nombre a cada polinomio:

- el polinomio arriba es el numerador
- el polinomio inferior es el denominador
Si tiene problemas para recordar, piense en denominador es abajo- ominador.
El método
Escríbelo cuidadosamente:

- el denominador va primero,
- luego un “)”,
- luego el numerador con una línea arriba
Ambos polinomios deben tener primero los términos de “orden superior” (aquellos con los exponentes más grandes , como el “2” en x 2 ).
Entonces:
 |
|
| Repita , utilizando el nuevo polinomio |
¡Es más fácil mostrar con un ejemplo!
Ejemplo:
Escríbelo cuidadosamente como a continuación, luego resuélvelo paso a paso (presiona play):
Verifique la respuesta:
Multiplica la respuesta por el polinomio inferior, deberíamos obtener el polinomio superior:
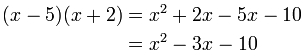
Restos
El ejemplo anterior funcionó perfectamente, ¡pero eso no siempre es así! Pruebe este:
Después de dividir nos quedamos con “2”, este es el “resto”.
El resto es lo que queda después de dividir.
Pero todavía tenemos una respuesta: pon el resto dividido por el polinomio inferior como parte de la respuesta, así:
Términos “faltantes”
Puede haber “términos faltantes” (ejemplo: puede haber una x 3 , pero no x 2 ). En ese caso, deje huecos o incluya los términos faltantes con un coeficiente de cero.
Ejemplo:
Escríbelo con coeficientes “0” para los términos faltantes, luego resuélvelo normalmente (presiona play):
¿Ves cómo necesitábamos un espacio para “3x 3 “?
Más de una variable
Hasta ahora hemos dividido polinomios con una sola variable ( x ), pero podemos manejar polinomios con dos o más variables (como x y y [ 19459032]) usando el mismo método.
Ejemplo:
