Secuencias
Puede leer una introducción suave a las Secuencias en Patrones de números comunes .
¿Qué es una secuencia?
Una secuencia es una lista de cosas (generalmente números) que están en orden.
Infinito o finito
Cuando la secuencia continúa para siempre se llama secuencia infinita ,
de lo contrario, es una secuencia finita
Ejemplos:
{1, 2, 3, 4, …} es una secuencia muy simple (y es una secuencia infinita )
{20, 25, 30, 35, …} también es una secuencia infinita
{1, 3, 5, 7} es la secuencia de los primeros 4 números impares (y es una secuencia finita )
{4, 3, 2, 1} es 4 a 1 al revés
{1, 2, 4, 8, 16, 32, …} es una secuencia infinita donde cada término se duplica
{a, b, c, d, e} es la secuencia de las primeras 5 letras alfabéticamente
{f, r, e, d} es la secuencia de letras en el nombre “fred”
{0, 1, 0, 1, 0, 1, …} es la secuencia de alternando 0s y 1s (sí, están en orden, es un orden alternativo en este caso)
En orden
Cuando decimos que los términos están “en orden”, ¡somos libres de definir qué orden es ! Podrían ir hacia adelante, hacia atrás … o podrían alternar … ¡o cualquier tipo de orden que queramos!
Como un conjunto
Una secuencia es como un conjunto , excepto:
- los términos son en orden (con Conjuntos, el orden no importa)
- el mismo valor puede aparecer muchas veces (solo una vez en Conjuntos)
Ejemplo: {0, 1, 0, 1, 0, 1, …} es la secuencia de alternar 0s y 1s.
El conjunto es solo {0,1}
Notación
| Las secuencias también usan la misma notación que los conjuntos: enumerar cada elemento, separados por una coma, y luego poner llaves alrededor de todo. |
{3, 5, 7, …} |
Los corchetes {} a veces se denominan “establecer corchetes” o “llaves”.
Una regla
Una secuencia generalmente tiene una regla , que es una forma de encontrar el valor de cada término.
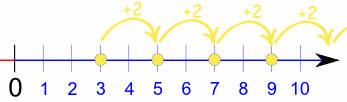
Ejemplo: la secuencia {3, 5, 7, 9, …} comienza en 3 y salta 2 cada vez:
Como fórmula
Decir “ comienza en 3 y salta 2 cada vez que ” está bien, pero no nos ayuda a calcular el:
- 10 a término,
- 100 a término, o
- n th término, donde n podría ser cualquier número de término que queramos.
Entonces, queremos una fórmula con “ n ” (donde n es cualquier número de término).
Entonces, ¿qué puede ser una regla para {3, 5, 7, 9, …}?
En primer lugar, podemos ver que la secuencia sube 2 cada vez, por lo que podemos adivinar que una Regla es algo así como “2 veces n” (donde “n” es el término número). Probémoslo:
Regla de prueba: 2n
| n | Plazo | Regla de prueba |
|---|---|---|
| 1 | 3 | 2 n = 2 × 1 = 2 |
| 2 | 5 | 2 n = 2 × 2 = 4 |
| 3 | 7 | 2 n = 2 × 3 = 6 |
Eso casi funcionó … pero es demasiado bajo en 1 cada vez, así que intentemos cambiarlo a:
Regla de prueba: 2n + 1
| n | Plazo | Regla de prueba |
|---|---|---|
| 1 | 3 | 2 n +1 = 2 × 1 + 1 = 3 |
| 2 | 5 | 2 n +1 = 2 × 2 + 1 = 5 |
| 3 | 7 | 2 n +1 = 2 × 3 + 1 = 7 |
¡Eso funciona!
Entonces, en lugar de decir “comienza en 3 y salta 2 cada vez”, escribimos esto:
2n + 1
Ahora podemos calcular, por ejemplo, el 100 ° término :
2 × 100 + 1 = 201
Muchas reglas
Pero las matemáticas son tan poderosas que podemos encontrar más de una Regla que funciona para cualquier secuencia.
Ejemplo: la secuencia {3, 5, 7, 9, …}
Acabamos de mostrar una regla para {3, 5, 7, 9, …} es: 2n + 1
Y así obtenemos: {3, 5, 7, 9, 11, 13, …}
¿Pero podemos encontrar otra regla?
¿Qué tal “números impares sin un 1 en ellos” :
Y obtenemos: {3, 5, 7, 9, 23, 25, …}
¡Una secuencia completamente diferente!
Y podríamos encontrar más reglas que coincidan {3, 5, 7, 9, …} . Realmente pudimos.
Por lo tanto, es mejor decir “Una regla” en lugar de “La regla” (a menos que sepamos que es la regla correcta).
Notación
Para facilitar el uso de reglas, a menudo utilizamos este estilo especial:
 |
|
Ejemplo: para mencionar el “quinto término”, escribimos: x 5
Entonces, una regla para {3, 5, 7, 9, …} se puede escribir como una ecuación como esta:
x n = 2n + 1
Y para calcular el décimo término podemos escribir:
x 10 = 2 n +1 = 2 × 10 +1 = 21
¿Puedes calcular x 50 (el término 50) haciendo esto?
Aquí hay otro ejemplo:
Ejemplo: Calcule los primeros 4 términos de esta secuencia:
{a n } = {(-1 / n) n }
Cálculos:
- a 1 = (-1/1) 1 = -1
- a 2 = (-1/2) 2 = 1/4
- a 3 = (-1/3) 3 = -1/27
- a 4 = (-1/4) 4 = 1/256
Respuesta:
{a n } = {-1, 1/4, -1/27, 1/256, …}
Secuencias especiales
Ahora veamos algunas secuencias especiales y sus reglas.
Secuencias aritméticas
En una Secuencia aritmética la diferencia entre un término y el siguiente es una constante .
En otras palabras, solo agregamos algún valor cada vez … al infinito.
Ejemplo:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, … |
Esta secuencia tiene una diferencia de 3 entre cada número.
Su regla es x n = 3n-2
En General podemos escribir una secuencia aritmética como esta:
{a, a + d, a + 2d, a + 3d, …}
donde:
- a es el primer término, y
- d es la diferencia entre los términos (llamada “diferencia común” )
Y podemos hacer la regla:
x n = a + d (n-1)
(Usamos “n-1” porque d no se usa en el primer término).
Secuencias geométricas
En una Secuencia geométrica cada término se encuentra por multiplicando el término anterior por una constante .
Ejemplo:
| 2, 4, 8, 16, 32, 64, 128, 256 , … |
Esta secuencia tiene un factor de 2 entre cada número.
Su regla es x n = 2 n
En General podemos escribir una secuencia geométrica como esta:
{a, ar, ar 2 , ar 3 , …}
donde:
- a es el primer término, y
- r es el factor entre los términos (llamado “relación común” )
Nota: r no debe ser 0.
- Cuando r = 0 , obtenemos la secuencia {a, 0,0, …} que no es geométrica
Y la regla es:
x n = ar (n-1)
(Usamos “n-1” porque ar 0 es el primer término)
Números triangulares
| 1, 3, 6, 10, 15, 21, 28, 36, 45 , … |
La Secuencia de números triangulares se genera a partir de un patrón de puntos que forman un
triángulo:

Al agregar otra fila de puntos y contar todos los puntos que podemos encontrar
El siguiente número de la secuencia.
Pero es más fácil usar esta regla:
x n = n (n + 1) / 2
Ejemplo:
- el quinto número triangular es x 5 = 5 (5 + 1) / 2 = 15 ,
- y el sexto es x 6 = 6 (6 + 1) / 2 = 21
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81 , … |
El siguiente número se hace al cuadrado donde está en el patrón.
La regla es x n = n 2
Números de cubo
| 1, 8, 27, 64, 125, 216, 343, 512, 729 , … |
El siguiente número se hace cubicando donde está en el patrón.
La regla es x n = n 3
Secuencia de Fibonacci
Esta es la Secuencia de Fibonacci
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 , … |
El siguiente número se encuentra al sumando los dos números anteriores juntos:
- El 2 se encuentra sumando los dos números anteriores (1 + 1)
- El 21 se encuentra sumando los dos números anteriores (8 + 13)
- etc …
La regla es x n = x n-1 + x n-2
Esa regla es interesante porque depende de los valores de los dos términos anteriores.
Reglas como esas se llaman fórmulas recursivas .
La secuencia de Fibonacci está numerada de 0 en adelante así:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| x n = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Ejemplo: el término “6” se calcula así:
x 6 = x 6-1 + x 6-2 = x 5 + x 4 = 5 + 3 = 8
Series y sumas parciales
Ahora que conoce las secuencias, lo siguiente que debe aprender es cómo resumirlas. Lea nuestra página en Sumas parciales .
Cuando sumamos solo parte de una secuencia, se denomina suma parcial .
Pero una suma de una secuencia infinita se llama “Serie” (suena como otro nombre para la secuencia, pero en realidad es una suma). Ver Infinite Series .
Ejemplo: números impares
Secuencia: {1, 3, 5, 7, …}
Serie: 1 + 3 + 5 + 7 + …
Suma parcial de los primeros 3 términos: 1 + 3 + 5

