
Secuencias: encontrar una regla
Para encontrar un número faltante en una secuencia, primero debemos tener una regla
Secuencia
Una secuencia es un conjunto de cosas (generalmente números) que están en orden.

Cada número de la secuencia se denomina término (o, a veces, “elemento” o “miembro”), lea Secuencias y series para obtener una discusión más detallada.
Encontrar números que faltan
Para encontrar un número faltante, primero encuentra una regla detrás de la secuencia.
A veces podemos mirar los números y ver un patrón:
Ejemplo: 1, 4, 9, 16,?
Respuesta: son Cuadrados (1 2 = 1, 2 2 = 4, 3 2 = 9, 4 [ 19459018] 2 = 16, …)
Regla: x n = n 2
Secuencia: 1, 4, 9, 16, 25, 36, 49, …
¿Viste cómo escribimos esa regla usando “x” y “n”?
x n significa “término número n”, por lo que el término 3 se escribe x 3
Y podemos calcular el término 3 usando:
x 3 = 3 2 = 9
Podemos usar una regla para encontrar cualquier término. Por ejemplo, el término 25 se puede encontrar “enchufando” 25 donde sea que esté n .
x 25 = 25 2 = 625
¿Qué tal otro ejemplo:
Ejemplo: 3, 5, 8, 13, 21,?
Después de 3 y 5, el resto son la suma de los dos números anteriores a ,
Eso es 3 + 5 = 8, 5 + 8 = 13, etc., que es parte de la Secuencia de Fibonacci :
3, 5, 8, 13, 21, 34, 55, 89, …
Que tiene esta regla:
Regla: x n = x n-1 + x n-2
Ahora, ¿qué significa x n-1 ? Significa “el término anterior” ya que el número de término n-1 es 1 menor que el número de término n .
Y x n-2 significa el término antes de ese .
Probemos esa regla para el sexto término:
x 6 = x 6-1 + x 6-2
x 6 = x 5 + x 4
Entonces el término 6 es igual al término 5 más el término 4. Ya sabemos que el término 5 es 21 y el término 4 es 13, entonces:
x 6 = 21 + 13 = 34
Muchas reglas
Uno de los problemas para encontrar “el próximo número” en una secuencia es que las matemáticas son tan poderosas que podemos encontrar más de una regla que funcione.
¿Cuál es el siguiente número en la secuencia 1, 2, 4, 7,?
Aquí hay tres soluciones (¡puede haber más!):
Solución 1: Agregar 1, luego agregar 2, 3, 4, …
Entonces, 1+ 1 = 2, 2+ 2 = 4, 4+ 3 = 7, 7+ 4 = 11, etc. …
Regla: x n = n (n-1) / 2 + 1
Secuencia: 1, 2, 4, 7, 11, 16, 22, …
(Esa regla parece un poco complicada, pero funciona)
Solución 2: después de 1 y 2, agregue los dos números anteriores, más 1:
Regla: x n = x n-1 + x n-2 + 1
Secuencia: 1, 2, 4, 7, 12, 20, 33, …
Solución 3: después de 1, 2 y 4, agregue los tres números anteriores
Regla: x n = x n-1 + x n-2 + x n-3 [ 19459005]
Secuencia: 1, 2, 4, 7, 13, 24, 44, …
Entonces, tenemos tres soluciones perfectamente razonables, y crean secuencias totalmente diferentes.
¿Cuál es el correcto? Están bien.
Y hay otras soluciones …
 |
… puede ser una lista de los números de los ganadores … así que el siguiente número podría ser … ¡cualquier cosa! |
Regla más simple
En caso de duda, elija la regla más simple que tenga sentido, pero también mencione que hay otras soluciones.
Encontrando diferencias
A veces ayuda encontrar las diferencias entre cada par de números … esto a menudo puede revelar un patrón subyacente.
Aquí hay un caso simple:
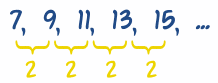
Las diferencias son siempre 2, por lo que podemos adivinar que “2n” es parte de la respuesta.
Probemos con 2n :
| n: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Términos (x n ): | 7 | 9 | 11 | 13 | 15 |
| 2n: | 2 | 4 | 6 | 8 | 10 |
| Incorrecto por: | 5 | 5 | 5 | 5 | 5 |
La última fila muestra que siempre estamos equivocados en 5, así que solo suma 5 y listo:
Regla: x n = 2n + 5
OK, podríamos haber calculado “2n + 5” simplemente jugando un poco con los números, pero queremos una forma sistemática de hacerlo, para cuando las secuencias se vuelvan más complicadas.
Segundas diferencias
En la secuencia {1, 2, 4, 7, 11, 16, 22, …} necesitamos encontrar las diferencias …
… y luego encuentra las diferencias de esas (llamadas segundas diferencias ), así:
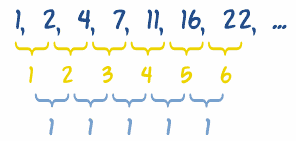
Las segundas diferencias en este caso son 1.
Con las segundas diferencias multiplicamos por n 2 2
En nuestro caso, la diferencia es 1, así que intentemos solo n 2 2 :
| n: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Términos (x n ): | 1 | 2 | 4 | 7 | 11 |
| n 2 2 : | 0,5 | 2 | 4,5 | 8 | 12,5 |
| Incorrecto por: | 0,5 | 0 | -0,5 | -1 | -1,5 |
Estamos cerca, pero parece que estamos a la deriva en 0.5, así que intentemos: n 2 2 – n 2
| n 2 2 – n 2 ] | 0 | 1 | 3 | 6 | 10 |
|---|---|---|---|---|---|
| Incorrecto por: | 1 | 1 | 1 | 1 | 1 |
Incorrecto por 1 ahora, así que agreguemos 1:
| n 2 2 – n 2 ] + 1 | 1 | 2 | 4 | 7 | 11 |
|---|---|---|---|---|---|
| Incorrecto por: | 0 | 0 | 0 | 0 | 0 |
¡Lo logramos!
La fórmula n 2 2 – n 2 + 1 se puede simplificar a n (n-1) / 2 + 1
Entonces, por “prueba y error” descubrimos una regla que funciona:
Regla: x n = n (n-1) / 2 + 1
Secuencia: 1, 2, 4, 7, 11, 16, 22, 29, 37, …
Otros tipos de secuencias
Lea Secuencias y series para obtener información sobre:
- Secuencias aritméticas
- Secuencias geométricas
- Secuencia de Fibonacci
- Secuencia triangular
Y también hay:
- Números primos
- Números factoriales
¡Y muchos más!
En verdad, hay demasiados tipos de secuencias para mencionar aquí, pero si hay una especial, le gustaría que agregue solo hágamelo saber .
