
Desviación estándar y varianza
La desviación solo significa qué tan lejos de lo normal
Desviación estándar
La desviación estándar es una medida de la propagación
nuestros números son
Su símbolo es σ (la letra griega sigma)
La fórmula es fácil: es la raíz cuadrada de la varianza . Entonces ahora preguntas, “¿Cuál es la varianza?”
Variación
La variación se define como:
El promedio de las diferencias al cuadrado de la media.
Para calcular la varianza, siga estos pasos:
- Calcule la Media (el promedio simple
de los números) - Luego, para cada número: resta la media y eleva al cuadrado el resultado
(la diferencia al cuadrado ). - Luego calcula el promedio de esas diferencias al cuadrado. ( Por qué
¿Cuadrado? )
Ejemplo
Tú y tus amigos acaban de medir la altura de tus perros
(en milímetros):
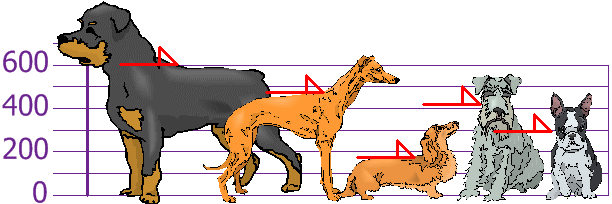
Las alturas (en los hombros) son: 600 mm, 470 mm, 170 mm, 430 mm
y 300 mm.
Encuentre la media, la varianza y la desviación estándar.
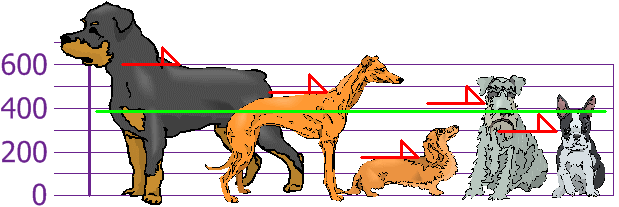
Su primer paso es encontrar la media:
Respuesta:
| Media | = | 600 + 470 + 170 + 430 + 300 5 |
| = | 1970 5 | |
| = | 394 |
por lo que la altura media (promedio) es de 394 mm. Tracemos esto en el gráfico:
Ahora calculamos la diferencia de cada perro de la media:
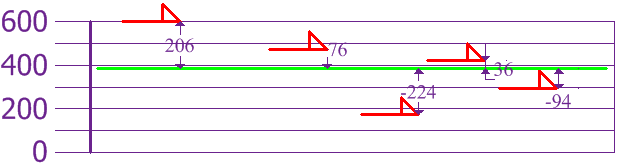
Para calcular la varianza, tome cada diferencia, cuadrátela y
luego promedia el resultado:
| Variación | ||
| σ 2 | = | 206 2 + 76 2 + (−224) 2 + 36 2 + (- 94) 2 5 |
| = | 42436 + 5776 + 50176 + 1296 + 8836 5 | |
| = | 108520 5 | |
| = | 21704 | |
Entonces la varianza es 21,704
Y la desviación estándar es solo la raíz cuadrada de la varianza,
entonces:
| Desviación estándar | ||
| σ | = | √21704 |
| = | 147,32 … | |
| = | 147 (al mm más cercano) | |
Y lo bueno de la desviación estándar es que es útil.
Ahora podemos mostrar qué alturas están dentro de una desviación estándar
(147 mm) de la media:
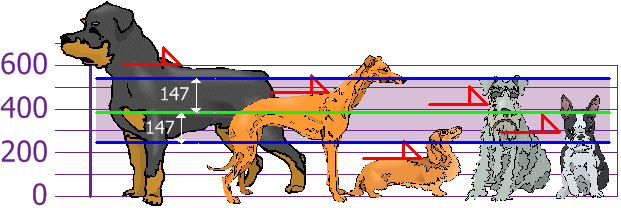
Entonces, usando la desviación estándar tenemos un “estándar”
forma de saber qué es normal y qué es extra grande o extra
pequeña.
Rottweilers son perros altos. Y los Dachshunds son un poco
corto, ¿verdad?
Usando

Podemos esperar que aproximadamente el 68% de los valores estén dentro de más o menos
1 desviación estándar.
Lea Distribución normal estándar para obtener más información.
Pruebe también la Calculadora de desviación estándar .
Pero … hay un pequeño cambio con Muestra Datos
Nuestro ejemplo ha sido para una Población (los 5 perros son los únicos perros en los que estamos interesados).
Pero si los datos son una muestra (una selección tomada de una población más grande), ¡entonces el cálculo cambia!
Cuando tiene valores de datos “N” que son:
- La población : dividir por N al calcular la varianza (como lo hicimos nosotros)
- Una muestra : dividir por N-1 al calcular la varianza
Todos los demás cálculos siguen siendo los mismos, incluida la forma en que calculamos la media.
Ejemplo: si nuestros 5 perros son solo una muestra de una población más grande de perros, dividimos por 4 en lugar de 5 así:
Piense en ello como una “corrección” cuando sus datos son solo una muestra.
Fórmulas
Aquí están las dos fórmulas, explicadas en Fórmulas de desviación estándar si desea saber más:
|
La “ Población Desviación estándar”: |
![square root of [ (1/N) times Sigma i=1 to N of (xi - mu)^2 ]](https://www.mathsisfun.com/data/images/standard-deviation-formula.gif) |
|
| La ” Muestra Desviación estándar “: | ![square root of [ (1/(N-1)) times Sigma i=1 to N of (xi - xbar)^2 ]](https://www.mathsisfun.com/data/images/standard-deviation-sample.gif) |
Parece complicado, pero el cambio importante es
dividir por N-1 (en lugar de N ) al calcular una varianza de muestra.
* Nota al pie: ¿Por qué cuadra las diferencias?
Si solo sumamos las diferencias de la media … los negativos cancelan los positivos:
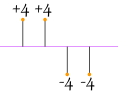 |
4 + 4 – 4 – 4 4 = 0 |
Entonces eso no funcionará. ¿Qué tal si usamos valores absolutos ?
 |
| 4 | + | 4 | + | −4 | + | −4 | 4 = 4 + 4 + 4 + 4 4 = 4 |
Eso se ve bien (y es la desviación media ), pero qué pasa con este caso:
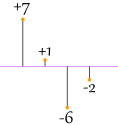 |
| 7 | + | 1 | + | −6 | + | −2 | 4 = 7 + 1 + 6 + 2 4 = 4 |
¡Oh, no! También da un valor de 4,
A pesar de que las diferencias están más extendidas.
Así que intentemos cuadrar cada diferencia (y tomar la raíz cuadrada al final):
 |
√ ( |
|
 |
√ ( 7 2 + 1 2 + 6 2 + 2 2 4 ) = √ ( 90 4 ) = 4,74 … |
¡Eso es bueno! La desviación estándar es mayor cuando las diferencias están más extendidas … justo lo que queremos.
De hecho, este método es una idea similar a la distancia entre puntos , recién aplicada de una manera diferente.
Y es más fácil usar álgebra en cuadrados y raíces cuadradas que valores absolutos, lo que hace que la desviación estándar sea fácil de usar en otras áreas de las matemáticas.
Volver al comienzo
