Correlación
Cuando dos conjuntos de datos están fuertemente vinculados, decimos que tienen una alta correlación .
La palabra Correlación está hecha de Co- (que significa “juntos”) y Relación
- La correlación es Positiva cuando los valores aumentan juntos y
- La correlación es Negativa cuando un valor disminuye a medida que el otro aumenta
Se supone que una correlación es lineal (siguiendo una línea).
La correlación puede tener un valor:
- 1 es una correlación positiva perfecta
- 0 no hay correlación (los valores no parecen vinculados en absoluto)
- -1 es una correlación negativa perfecta
El valor muestra qué tan buena es la correlación (no qué tan empinada es la línea) y si es positiva o negativa.
Ejemplo: venta de helados
La heladería local realiza un seguimiento de la cantidad de helado que venden en comparación con la temperatura de ese día, aquí están sus cifras de los últimos 12 días:
| Ventas de helados frente a temperatura | |
| Temperatura ° C | Venta de helados |
|---|---|
| 14,2 ° | $ 215 |
| 16,4 ° | $ 325 |
| 11,9 ° | $ 185 |
| 15,2 ° | $ 332 |
| 18,5 ° | $ 406 |
| 22,1 ° | $ 522 |
| 19,4 ° | $ 412 |
| 25,1 ° | $ 614 |
| 23,4 ° | $ 544 |
| 18,1 ° | $ 421 |
| 22,6 ° | $ 445 |
| 17.2 ° | $ 408 |
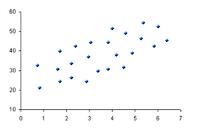
Y aquí están los mismos datos que un Diagrama de dispersión :

Podemos ver fácilmente que el clima más cálido y las mayores ventas van de la mano. La relación es buena pero no perfecta.
De hecho, la correlación es 0,9575 … mira al final cómo lo calculé.
Pruebe también la Calculadora de correlación .
La correlación no es buena en las curvas
El cálculo de correlación solo funciona correctamente para las relaciones de línea recta.
Nuestro ejemplo de helado: ¡ha habido una ola de calor!
Hace tanto calor que la gente no se acerca a la tienda, y las ventas comienzan a caer .
Aquí está el último gráfico:

El valor de correlación es ahora 0 : “Sin correlación” …!
El valor de correlación calculado es 0 (lo resolví), lo que significa “sin correlación”.
Pero podemos ver que los datos siguen una bonita curva que alcanza un pico alrededor de los 25 ° C
Pero el cálculo de la correlación no es lo suficientemente “inteligente” como para ver esto.
Moraleja de la historia: haz un diagrama de dispersión , ¡y míralo!
Puede ver una relación que el cálculo no ve.
“La correlación no es causal”
Un dicho común es “La correlación no es causalidad”.
Lo que realmente significa es que una correlación no prueba una cosa causa la otra:
- Una cosa podría causar la otra
- El otro podría causar que ocurra el primero
- Pueden estar vinculados por algo diferente
- ¡O podría ser una casualidad!
Puede haber muchas razones por las cuales los datos tienen una buena correlación.
Ejemplo: gafas de sol vs helado
Nuestra tienda de helados encuentra cuántas gafas de sol fueron vendidas por una gran tienda por día y las compara con sus ventas de helados:

La correlación entre las gafas de sol y las ventas de helados es alta
¿Esto significa que las gafas de sol hacen que la gente quiera helado?
Ejemplo: los suburbios pobres tienen más probabilidades de tener una alta contaminación.
¿Por qué?
- ¿Contaminan los pobres?
- ¿Son los suburbios contaminados el único lugar donde la gente pobre puede pagar?
- ¿Es un vínculo común, como fábricas con trabajos mal pagados y mucha contaminación?
Ejemplo: un caso real!
Hace unos años, una encuesta de empleados encontró una fuerte correlación positiva entre “Estudiar un curso externo” y Días de enfermedad .
Significa esto:
- ¿Estudiar los enferma?
- ¿Las personas enfermas estudian mucho?
- ¿O mintieron acerca de estar enfermos para poder estudiar más?
Sin más investigación no podemos estar seguros de por qué.
Cómo calcular
¿Cómo calculé el valor 0,9575 en la parte superior?
Usé “Correlación de Pearson”. Existe un software que puede calcularlo, como la función CORREL () en Excel o LibreOffice Calc …
… pero aquí es cómo calcularlo usted mismo:
Llamemos a los dos conjuntos de datos “x” e “y” (en nuestro caso, la temperatura es x y la venta de helados es y ):
- Paso 1: Encuentre la media de x y la media de y
- Paso 2: reste la media de x de cada valor de x (llámelos “ a “) y reste la media de y de cada valor de y (llámelos “ b “)
- Paso 3: Calcular: ab , a 2 y b 2 para cada valor [19459011 ]
- Paso 4: Suma ab , suma a 2 y suma b 2 [ 19459011]
- Paso 5: Divida la suma de ab por la raíz cuadrada de [(suma de a 2 ) × (suma de b 2 )]
Así es como calculé el primer ejemplo de Ice Cream (valores redondeados a 1 o 0 decimales):

Como fórmula es:
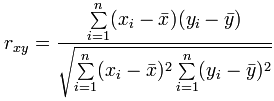
Dónde:
- Σ es Sigma , el símbolo para “resumir”
-
es cada valor de x menos la media de x (llamada “a” arriba)
-
es cada valor de y menos la media de y (llamada “b” arriba)
Probablemente no tenga que calcularlo así, pero al menos sabe que no es “mágico”, sino simplemente un conjunto de cálculos de rutina.
Nota para programadores
Puede calcularlo de una sola vez a través de los datos. Solo suma x , y , x 2 , y 2 y [ 19459004] xy (no es necesario para a o b cálculos anteriores) luego use la fórmula:
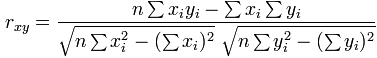
Otros métodos
Hay otras formas de calcular un coeficiente de correlación, como el “coeficiente de correlación de rango de Spearman”.

