Probabilidad: eventos independientes

¡La vida está llena de eventos aleatorios!
Debes tener una “sensación” para que sean una persona inteligente y exitosa.
El lanzamiento de una moneda, el lanzamiento de dados y los sorteos de lotería son ejemplos de eventos aleatorios.
Puede haber:
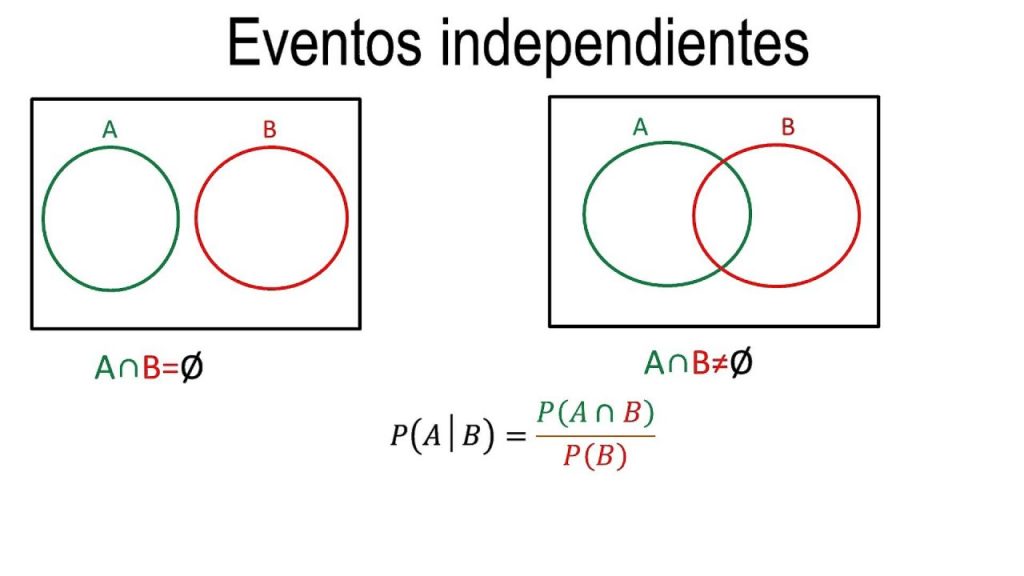
Eventos independientes

Los eventos independientes no se ven afectados por eventos anteriores.
¡Esta es una idea importante!
Una moneda no “sabe” que salió cara antes.
Y cada lanzamiento de una moneda es una cosa aislada perfecta.
Ejemplo: arrojas una moneda y aparece “Cara” tres veces … ¿cuál es la posibilidad de que el próximo lanzamiento también sea una “Cabeza”?
La posibilidad es simplemente ½ (o 0.5) como CUALQUIER lanzamiento de la moneda.
¡Lo que hizo en el pasado no afectará el lanzamiento actual!
Algunas personas piensan que “es una cola atrasada”, pero realmente el próximo lanzamiento de la moneda es totalmente independiente de cualquier lanzamiento anterior.
Al decir “se debe una cola”, o “solo una vez más, mi suerte se debe al cambio” se llama La falacia del jugador
Por supuesto, su suerte puede cambiar , porque cada lanzamiento de la moneda tiene la misma probabilidad.
Probabilidad de eventos independientes
“Probabilidad” (o “Chance”) es cuán probable algo va a suceder.
Entonces, ¿cómo calculamos la probabilidad?
Probabilidad de que ocurra un evento =
Número de formas en que puede suceder
Número total de resultados

Ejemplo: ¿cuál es la probabilidad de obtener una “Cabeza” al lanzar una moneda?
Número de formas en que puede suceder: 1 (Cabeza)
Número total de resultados: 2 (Cabeza y cola)
Entonces la probabilidad =
1
2
= 0,5

Ejemplo: ¿cuál es la probabilidad de obtener un “4” o “6” al tirar un dado?
Número de formas en que puede suceder: 2 (“4” y “6”)
Número total de resultados: 6 (“1”, “2”, “3”, “4”, “5” y “6”)
Entonces la probabilidad =
2
6
=
1
3
= 0,333 …
Formas de mostrar probabilidad
La probabilidad va de 0 (imposible) a 1 (cierto):

A menudo se muestra como una fracción decimal o .
Ejemplo: la probabilidad de obtener una “Cabeza” al lanzar una moneda:
- Como un decimal: 0,5
- Como una fracción: 1/2
- Como porcentaje: 50%
- O a veces así: 1 en 2
Dos o más eventos
Podemos calcular las posibilidades de dos o más eventos independientes por multiplicando las posibilidades.
Ejemplo: probabilidad de 3 cabezas seguidas
Por cada lanzamiento de una moneda, una Cabeza tiene una probabilidad de 0.5:

Y así, la posibilidad de obtener 3 cabezas seguidas es 0,125
Por lo tanto, cada lanzamiento de una moneda tiene una probabilidad de ½ de ser Caras, pero muchas Caras seguidas es poco probable.
Ejemplo: ¿Por qué es improbable obtener, por ejemplo, 7 caras seguidas, cuando cada lanzamiento de una moneda tiene una probabilidad ½ de ser Cabezas?
Porque estamos haciendo dos preguntas diferentes:
Pregunta 1: ¿Cuál es la probabilidad de 7 caras seguidas?
Pregunta 2: Cuando acabamos de obtener 6 caras seguidas, ¿cuál es la probabilidad de que el próximo lanzamiento sea también una cabeza?
Puedes jugar con el Quincunx para ver cuántos efectos independientes aún pueden tener un patrón.
Notación
Usamos “P” para significar “Probabilidad de”,
Entonces, para eventos independientes:
P (A y B) = P (A) × P (B)
La probabilidad de A y B es igual a la probabilidad de A multiplicada por la probabilidad de B
Ejemplo: su jefe (para ser justos) asigna aleatoriamente a todos 2 horas adicionales de trabajo en las noches de fin de semana entre las 4 y la medianoche.
¿Cuáles son las posibilidades que tienes el sábado entre las 4 y las 6?

Día: hay dos días en el fin de semana, entonces P (sábado) = 0.5
Hora: desea las 2 horas de “4 a 6”, de las 8 horas de 4 a medianoche):
P (“4 a 6”) = 2/8 = 0.25
Y:
| P (sábado y “4 a 6”) | = P (sábado) × P (“4 a 6”) |
| = 0,5 × 0,25 | |
| = 0,125 |
O una probabilidad del 12,5%
(Nota: TAMBIÉN podríamos haber calculado que quería 2 horas de un total de 16 horas posibles, que es 2/16 = 0.125. Ambos métodos funcionan aquí.)
Otro ejemplo
Ejemplo: la posibilidad de que un vuelo se retrase es 0.2 (= 20%), ¿cuáles son las posibilidades de que no haya demoras en un viaje de ida y vuelta
La posibilidad de que un vuelo no tenga un retraso es 1 – 0.2 = 0.8 , así que estos son todos los resultados posibles:
| 0.8 × 0.8 = | 0,64 posibilidad de sin demoras | |
| 0.2 × 0.8 = | 0,16 posibilidad de 1er vuelo retrasado | |
| 0.8 × 0.2 = | 0,16 posibilidad de retraso en el vuelo de regreso | |
| 0.2 × 0.2 = | 0.04 posibilidad de retrasar ambos vuelos |
Cuando sumamos todas las posibilidades que obtenemos:
0.64 + 0.16 + 0.16 + 0.04 = 1.0
Todos se suman a 1.0, que es una buena manera de verificar nuestros cálculos.
Resultado: 0.64 , o un 64% de probabilidad de que no haya demoras
Un ejemplo más
Imagina que hay dos grupos:
- Un miembro de cada grupo es elegido al azar para el círculo de ganadores,
- luego uno de esos es elegido al azar para obtener el gran premio en dinero:

¿Cuál es su probabilidad de ganar el gran premio?
- hay una posibilidad de 1/5 de ir al círculo de ganadores
- y una 1/2 oportunidad de ganar el gran premio
Entonces tienes una probabilidad de 1/5 seguida de una oportunidad de 1/2 … lo que hace una probabilidad de 1/10 en general:
1 5 × 1 2 = ] 1 5 × 2 = 1 10
O podemos calcular usando decimales (1/5 es 0.2 y 1/2 es 0.5):
0.2 x 0.5 = 0.1
Entonces, su probabilidad de ganar mucho dinero es 0.1 (que es lo mismo que 1/10).
¡Coincidencia!
Muchas “coincidencias” son, de hecho, probables.
Ejemplo: estás en una habitación con 30 personas y descubres que Zach y Anna celebran su cumpleaños el mismo día.
¿Dices:
- “¡Guau, qué extraño!”, O
- “Eso parece razonable, con tanta gente aquí”
De hecho, existe un 70% de probabilidad de que suceda … así que es probable .

¿Por qué es tan alta la posibilidad?
Porque estás comparando a todos con los demás (no solo de uno a muchos).
Y con 30 personas eso es 435 comparaciones
(Lea Cumpleaños compartidos para obtener más información)
Ejemplo: Snap!
¿Alguna vez dijiste algo exactamente al mismo tiempo que otra persona ?
¡Guau, qué increíble!
Pero probablemente estabas compartiendo una experiencia (película, viaje, lo que sea) y tus pensamientos eran similares.
Y hay tantas maneras de decir algo …
… así que es como el juego de cartas “Snap!” (también llamado Slaps o Slapjack) …
… si pronuncian suficientes palabras juntas, eventualmente coincidirán.
Entonces, tal vez no sea tan sorprendente, solo una simple oportunidad en el trabajo.
¿Puedes pensar en otros casos donde una “coincidencia” era simplemente una cosa probable?
Conclusión
- La probabilidad es: (Número de formas en que puede suceder) / (Número total de resultados)
- Los eventos dependientes (como quitar canicas de una bolsa) se ven afectados por eventos anteriores
- Los eventos independientes (como el lanzamiento de una moneda) no se ven afectados por eventos anteriores
- Podemos calcular la probabilidad de dos o más Eventos independientes por multiplicando
- No todas las coincidencias son realmente improbables (cuando piensas en ellas).
