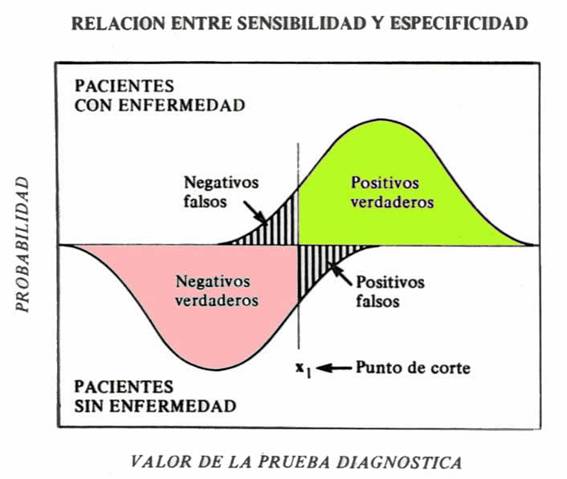
Falsos positivos y falsos negativos
La prueba dice “Sí” … ¿o sí?
Cuando tiene un examen que puede decir “Sí” o “No” (como un examen médico), debe pensar:
- Podría ser incorrecto cuando dice “Sí”.
- Podría ser incorrecto cuando dice “No”.
¿Mal?
¡Es como si te dijeran que hiciste algo cuando tú no !
O no lo hiciste cuando realmente lo hiciste.
Cada uno tiene un nombre especial: “Falso positivo” y “Falso negativo” :
| Dicen que hiciste | Dicen que no | |
| Realmente lo hiciste | ¡Tienen razón! | “Falso negativo” |
| Realmente no lo hiciste | “Falso positivo” | ¡Tienen razón! |
Estos son algunos ejemplos de “falsos positivos” y “falsos negativos”:
- Seguridad del aeropuerto : un “falso positivo” es cuando elementos ordinarios como llaves o monedas se confunden con armas (la máquina emite un “pitido”)
- Control de calidad : un “falso positivo” es cuando un artículo de buena calidad es rechazado, y un “falso negativo” es cuando un artículo de mala calidad es aceptado. (Un resultado “positivo” significa que hay un defecto.)
- Software antivirus : un “falso positivo” es cuando se cree que un archivo normal es un virus
- Examen médico : las pruebas de bajo costo que se realizan a un grupo grande pueden dar muchos falsos positivos (decir que tiene una enfermedad cuando no la tiene) y luego pedirle que se haga pruebas más precisas.
Pero muchas personas no entienden los números verdaderos detrás de “Sí” o “No”, como en este ejemplo:

Ejemplo: ¿alergia o no?
Hunter dice que le pica. Hay una prueba de alergia a los gatos, pero esta prueba no siempre es correcta:
- Para las personas que realmente tienen tienen alergia, la prueba dice “Sí” 80% de las veces
- Para las personas que no tienen alergia, la prueba dice “Sí” 10% del tiempo (“falso positivo”)
Aquí está en una tabla:
| La prueba dice “Sí” | La prueba dice “No” | |
| Tiene alergia | 80% | 20% “Falso negativo” |
| No lo tengo | 10% “falso positivo” | 90% |
Pregunta: Si el 1% de la población tiene alergia, y La prueba de Hunter dice “Sí” ,
¿Cuáles son las posibilidades de que Hunter realmente tenga la alergia?
¿Crees que el 75%? O tal vez el 50%?
Se realizó una prueba similar a los médicos y la mayoría adivinó alrededor del 75% …
…
¡pero estaban muy equivocados!
(Fuente: “Razonamiento probabilístico en medicina clínica: problemas y oportunidades” por David M. Eddy 1982, en el que se basa este ejemplo)
Hay tres formas diferentes de resolver esto:
- “Imagine a 1000”,
- “Diagramas de árbol” o
- “Teorema de Bayes”,
usa el que prefieras. Miremos ahora:
Intenta imaginar a mil personas
Cuando intentes comprender preguntas como esta, solo imagina un grupo grande (digamos 1000) y juega con los números:
- De 1000 personas, solo 10 realmente tienen alergia (1% de 1000 es 10)
- La prueba es 80% correcta para las personas que tienen alergia, por lo que obtendrá 8 de esos 10 correctos .
- Pero 990 no tienen alergia, y la prueba dirá “Sí” al 10% de ellos,
que es 99 personas dice “Sí” a erróneamente (falso positivo) - Entonces, de 1000 personas, la prueba dice “ Sí ” a (8 + 99) = 107 personas
Como tabla:
| Incluido en el 1% | La prueba dice “Sí” | La prueba dice “No” | |
| Tiene alergia | 10 | 8 | 2 |
| No lo tengo | 990 | 99 | 891 |
| 1000 | 107 | 893 |
Entonces 107 personas obtienen un “Sí” pero solo 8 de ellos realmente tienen alergia:
8/107 = aproximadamente 7%
Entonces, aunque la prueba de Hunter dijo “Sí”, todavía es 7% probable que Hunter tiene una alergia a los gatos.
¿Por qué tan pequeño? Bueno, la alergia es tan rara que aquellos que realmente la tienen son muy superados en número por aquellos con un falso positivo.
Como un árbol
Dibujar un diagrama de árbol realmente puede ayudar:

Primero que nada, verifiquemos que todos los porcentajes sumen:
0.8% + 0.2% + 9.9% + 89.1% = 100% (¡bien!)
Y las dos respuestas “Sí” suman 0.8% + 9.9% = 10.7% , pero solo 0.8% son correctas.
0.8 / 10.7 = 7% (misma respuesta que la anterior)
Teorema de Bayes
El teorema de Bayes tiene una fórmula especial para este tipo de cosas:
P (A | B) = P (A) P (B | A) P (A) P (B | A) + P (no A) P ( B | no A)
donde:
- P significa “Probabilidad de”
- | significa “dado que”
- A en este caso es “en realidad tiene alergia”
- B en este caso es “la prueba dice que sí”
Entonces:
P (A | B) significa “La probabilidad de que Hunter realmente tenga la alergia dado que la prueba dice Sí”
P (B | A) significa “La probabilidad de que la prueba diga Sí dado que Hunter realmente tiene la alergia”
Para ser más claros, cambiemos A a tiene (en realidad tiene alergia) y B a Sí (la prueba dice que sí):
P (tiene | Sí) = P (tiene) P (Sí | tiene) P (tiene) P (Sí | tiene) + P (no tiene) P ( Sí | no tiene)
Y pon los números:
P (tiene | sí) = 0.01 × 0.8 0.01 × 0.8 + 0.99 × 0.1
= 0,0748 …
Que es aproximadamente 7%
Obtenga más información sobre esto en Bayes ‘Theorem .
Un último ejemplo
Ejemplo extremo: virus informático

Un virus informático se propaga por todo el mundo y todos informan a una computadora maestra.
Los buenos capturan la computadora maestra y descubren que un millón de computadoras han sido infectadas (pero no saben cuáles).
¡Los gobiernos deciden tomar medidas!
Nadie puede usar Internet hasta que su computadora pase la prueba “libre de virus”. La prueba es 99% precisa (bastante buena, ¿verdad?) Pero el 1% de las veces dice que tiene el virus cuando no lo tiene (un “falso positivo”).
Ahora digamos que hay 1000 millones de usuarios de internet.
- De 1 millón con el virus, el 99% de ellos están prohibidos correctamente = aproximadamente 1 millón
- Pero los falsos positivos son 999 millones x 1% = aproximadamente 10 millones
Entonces, un total de 11 millones están prohibidos, pero solo 1 de esos 11 en realidad tienen el virus.
Entonces, si te banean, ¡solo hay un 9% de posibilidades de que tengas el virus!
Conclusión
Al tratar con falsos positivos y falsos negativos (u otras preguntas de probabilidad difíciles) podemos usar estos métodos:
- Imagina que tienes 1000 (de lo que sea),
- Haz un diagrama de árbol o
- Usa el teorema de Bayes
