
Regresión de mínimos cuadrados
Línea de mejor ajuste
Imagina que tienes algunos puntos y quieres tener una línea que se ajuste mejor a ellos de esta manera:

Podemos colocar la línea “a ojo”: trate de tener la línea lo más cerca posible de todos los puntos, y un número similar de puntos arriba y debajo de la línea.
Pero para una mayor precisión, veamos cómo calcular la línea usando Regresión de mínimos cuadrados .
La línea
Nuestro objetivo es calcular los valores m (pendiente) y b (intersección en y) en la ecuación de una línea :
Donde:
- y = qué tan lejos
- x = qué tan avanzado
- m = Pendiente o Gradiente (cuán empinada es la línea)
- b = la Intercepción Y (donde la línea cruza el eje Y)
Pasos
Para encontrar la línea de mejor ajuste para N puntos:
Paso 1 : Para cada punto (x, y) calcule x 2 y xy
Paso 2 : Suma todos x, y, x 2 y xy, lo que nos da Σx, Σy, Σx 2 y Σxy ( Σ significa “resumir” )
Paso 3 : Calcular pendiente m :
m = N Σ (xy) – Σx Σy N Σ (x 2 ) – (Σx) 2
(N es el número de puntos)
Paso 4 : Calcular intercepción b :
b = Σy – m Σx N
Paso 5 : Ensamble la ecuación de una línea
y = mx + b
¡Listo!
Ejemplo
¡Tengamos un ejemplo para ver cómo hacerlo!

Ejemplo: Sam descubrió cuántas horas de sol frente a cuántos helados se vendieron en la tienda de lunes a viernes:
| “x” Horas de sol |
“y” Helados vendidos |
|---|---|
| 2 | 4 |
| 3 | 5 |
| 5 | 7 |
| 7 | 10 |
| 9 | 15 |
Encontremos el mejor m (pendiente) y b (intersección en y) que se ajusta a esos datos
y = mx + b
Paso 1 : Para cada (x, y) calcule x 2 y xy:
| x | y | x 2 | xy |
|---|---|---|---|
| 2 | 4 | 4 | 8 |
| 3 | 5 | 9 | 15 |
| 5 | 7 | 25 | 35 |
| 7 | 10 | 49 | 70 |
| 9 | 15 | 81 | 135 |
Paso 2 : Suma x, y, x 2 y xy (nos da Σx, Σy, Σx 2 y Σxy):
| x | y | x 2 | xy |
|---|---|---|---|
| 2 | 4 | 4 | 8 |
| 3 | 5 | 9 | 15 |
| 5 | 7 | 25 | 35 |
| 7 | 10 | 49 | 70 |
| 9 | 15 | 81 | 135 |
| Σx: 26 | Σy: 41 | Σx 2 : 168 | Σxy: 263 |
También N (número de valores de datos) = 5
Paso 3 : Calcular pendiente m :
m = N Σ (xy) – Σx Σy
N Σ (x 2 ) – (Σx) 2
= 5 x 263 – 26 x 41 5 x 168 – 26 2
= 1315 – 1066 840 – 676
= 249 164 = 1,5183 …
Paso 4 : Calcular intercepción b :
b =
Σy – m Σx
N
=
41 – 1,5183 x 26
5
= 0,3049 …
Paso 5 : Ensamble la ecuación de una línea:
y = mx + b
y = 1.518x + 0.305
Veamos cómo funciona:
| x | y | y = 1.518x + 0.305 | error |
|---|---|---|---|
| 2 | 4 | 3,34 | −0,66 |
| 3 | 5 | 4,86 | −0,14 |
| 5 | 7 | 7,89 | 0,89 |
| 7 | 10 | 10,93 | 0,93 |
| 9 | 15 | 13,97 | −1,03 |
Aquí están los puntos (x, y) y la línea y = 1.518x + 0.305 en un gráfico:
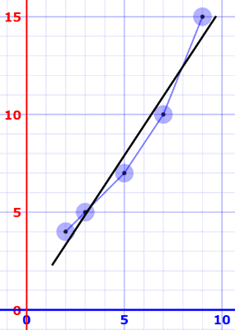
¡Buen ajuste!
Sam escucha el pronóstico del tiempo que dice “esperamos 8 horas de sol mañana”, por lo que utiliza la ecuación anterior para estimar que venderá
y = 1.518 x 8 + 0.305 = 12.45 Helados
Sam hace una mezcla fresca de cono de waffle para 14 helados por si acaso. Mmm
¿Cómo funciona?
Funciona haciendo que el total de cuadrado de los errores sea lo más pequeño posible (es por eso que se llama “mínimos cuadrados”):

La línea recta minimiza la suma de los errores al cuadrado
Entonces, cuando cuadramos cada uno de esos errores y los sumamos, el total es lo más pequeño posible.
Puede imaginar (pero no con precisión) cada punto de datos conectado a una barra recta por resortes:

Boing!
Valores atípicos
¡Ten cuidado! Los mínimos cuadrados son sensibles a valores atípicos . Un valor extraño tirará de la línea hacia él.
Usa la aplicación
Juega con la Calculadora de mínimos cuadrados
No solo para líneas
Esta idea puede usarse en muchas otras áreas, no solo en líneas.

Un “círculo de mejor ajuste”
¡Pero las fórmulas (y los pasos dados) serán muy diferentes!
