
La evolución de los números
Quiero llevarte a una aventura …
… una aventura a través del mundo de los números.
Comencemos por el principio:
P: ¿Cuál es la idea más simple de un número?
A: ¡Algo con lo que cuenta !
Los números de conteo
Podemos usar números para contar : 1, 2, 3, 4, etc.
Los humanos han estado usando números para contar por miles de años. Es algo muy natural de hacer.
- Puedes tener “ 3 amigos”,
- un campo puede tener “ 6 vacas”
- y así sucesivamente.
Entonces tenemos:
Contar números: {1, 2, 3, …}
Y los “números de conteo” satisfacían a las personas durante mucho tiempo.
Cero
La idea de cero , aunque natural para nosotros ahora, no era natural para los humanos primitivos … si no hay nada que contar, ¿cómo podemos contarlo?
Ejemplo: podemos contar perros, pero no podemos contar un espacio vacío:
 |
 |
|
| Dos perros | ¿Cero perros? Cero gatos? |
|---|
¡Un parche de hierba vacío es solo un parche de hierba vacío!
Marcador de posición
Pero hace unos 3.000 años la gente necesitaba distinguir entre números como 4 y 40. ¡Sin el cero se ven iguales!
Entonces usaron un “marcador de posición”, un espacio o símbolo especial, para mostrar que “no hay dígitos aquí”
| 5 2 |
Entonces “5 2” significaba “502” (5 cientos, nada para las decenas y 2 unidades) |
Número
La idea de cero había comenzado, pero no fue por otros mil años más o menos que la gente comenzó a pensar en ella como un número real .
Pero ahora podemos pensar
“¡Tenía 3 naranjas, luego me comí las 3 naranjas, ahora tengo cero naranjas …!”
Los números enteros
Entonces, agreguemos cero a los números de conteo para hacer un nuevo conjunto de números.
Pero necesitamos un nuevo nombre, y ese nombre es “Números enteros”:
Números enteros : {0, 1, 2, 3, …}

Los números naturales
También puede escuchar el término “ Números naturales ” … que puede significar:
- los “números de conteo”: {1, 2, 3, …}
- o los “números enteros”: {0, 1, 2, 3, …}
dependiendo del tema. Supongo que no están de acuerdo sobre si cero es “natural” o no.
Números negativos
¡Pero la historia de las matemáticas se trata de personas que hacen preguntas y buscan las respuestas!
Una de las buenas preguntas para hacer es
“si podemos ir en una dirección, ¿podemos ir en dirección opuesta ?”
Podemos contar hacia adelante: 1, 2, 3, 4, …
|
… pero qué pasa si contamos al revés: 3, 2, 1, 0, … ¿qué pasa después? |
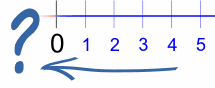 |
La respuesta es: obtenemos números negativos:

Ahora podemos avanzar y retroceder tanto como queramos
Pero, ¿cómo puede un número ser “negativo”?
Simplemente siendo menor que cero.
|
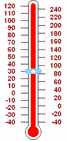
Un ejemplo simple es la temperatura . Definimos cero grados Celsius ( 0 ° C ) cuando el agua se congela … pero si nos ponemos más fríos necesitamos temperaturas negativas. Entonces -20 ° C está 20 ° por debajo de cero. |

¿Vacas negativas?
¡Y en teoría podemos tener una vaca negativa!
Piensa en esto … Si acabas de vendiste dos toros , pero solo puedes encontrar uno para entregar al nuevo propietario … en realidad tienes menos un toro … ¡estás en deuda con un toro!
Entonces existen números negativos, y vamos a necesitar un nuevo conjunto de números para incluirlos …
Enteros
Si incluimos los números negativos con los números enteros, tenemos un nuevo conjunto de números que se denominan enteros
Enteros: {…, -3, -2, -1, 0, 1, 2, 3, …}
Los números enteros incluyen cero, los números de conteo y el negativo de los números de conteo, para hacer una lista de números que se extienden en cualquier dirección indefinidamente.

Fracciones

Si tienes una naranja y quieres compartirla con alguien, debes cortarla por la mitad.
¡Acabas de inventar un nuevo tipo de número!
Tomaste un número (1) y lo dividiste por otro número (2) para obtener la mitad (1/2)
Lo mismo sucede cuando tenemos cuatro galletas (4) y queremos compartirlas entre tres personas (3) … obtienen (4/3) galletas cada una.
Un nuevo tipo de número y un nuevo nombre:
Números racionales
Cualquier número que se pueda escribir como fracción se llama Número racional.
Entonces, si “p” y “q” son enteros (recuerde que hablamos de enteros), entonces p / q es un número racional.
Ejemplo: si p es 3 y q es 2, entonces:
p / q = 3/2 = 1.5 es un número racional
La única vez que esto no funciona es cuando q es cero, porque dividiendo por cero no está definido.
Números racionales : {p / q: py q son enteros, q no es cero}
Entonces la mitad ( ½ ) es un número racional.
Y 2 es un número racional también, porque podríamos escribirlo como 2/1
Entonces, los números racionales incluyen:
- todos los enteros
- y todas las fracciones .
Incluso un número como 13.3168980325 es un número racional.
13.3168980325 = 133,168,980,325 / 10,000,000,000
Eso parece incluir todos los números posibles, ¿verdad?
Pero hay más
La gente no dejó de hacer preguntas … y aquí hay una que causó mucho escándalo durante la época de Pitágoras:
 |
Si dibujamos un cuadrado (de tamaño “1”), ¿cuál es la distancia a través de la diagonal? |
La respuesta es la raíz cuadrada de 2 , que es 1.4142135623730950 … (etc)
Pero no es un número como 3, o cinco tercios, o algo así …
… de hecho, no podemos responder esa pregunta usando una razón de dos enteros
raíz cuadrada de 2 ≠ p / q
… y entonces no es un número racional (lea más aquí )
¡Guau! ¡Hay números que NO son números racionales! ¿Cómo los llamamos?
¿Qué es “No racional” …? ¡Irracional!
Números irracionales
Entonces, la raíz cuadrada de 2 (√2) es un número irracional . Se llama irracional porque no es racional (no se puede hacer usando una relación simple de enteros). No es una locura ni nada, simplemente no es racional.
Y sabemos que hay muchos más números irracionales. Pi ( π ) es famoso.
Útil
Entonces los números irracionales son útiles. Los necesitamos para
- encuentra la distancia diagonal a través de algunos cuadrados,
- para calcular muchos cálculos con círculos (usando π ),
- y más,
Así que realmente deberíamos incluirlos.
Y así, presentamos un nuevo conjunto de números …
Números reales
Así es, ¡otro nombre!
Los números reales incluyen:
- los números racionales y
- los números irracionales
Números reales: {x: x es un número racional o irracional}
De hecho, un número real puede considerarse como cualquier punto en cualquier lugar de la recta numérica:
Esto solo muestra unos pocos decimales (es solo una computadora simple)
¡pero los números reales pueden tener muchos más decimales !
Cualquier punto En cualquier lugar en la recta numérica, ¡eso seguramente son suficientes números!
Pero hay un número más que resultó ser muy útil. Y una vez más, vino de una pregunta.
Imagina …
La pregunta es:
“¿hay una raíz cuadrada de menos una ?”
En otras palabras, ¿qué podemos multiplicar por sí mismos para obtener -1 ?
Piensa en esto: si multiplicamos cualquier número por sí mismo no podemos obtener un resultado negativo:
- 1 × 1 = 1 ,
- y también (-1) × (-1) = 1 (porque un negativo por un negativo da un positivo )
Entonces, ¿qué número, cuando se multiplica por sí mismo, resulta en -1 ?
Esto normalmente no es posible, pero …
“si puedes imaginarlo, entonces puedes jugar con él”
Entonces, …
Números imaginarios
 |
… imaginemos que la raíz cuadrada de menos uno existe . Incluso podemos darle un símbolo especial: la letra i |
Y podemos usarlo para responder preguntas:
Ejemplo: ¿cuál es la raíz cuadrada de -9?
Respuesta: √ (-9) = √ (9 × -1) = √ (9) × √ (-1) = 3 × √ (-1) = 3 i
OK, la respuesta aún involucra i , pero da una respuesta sensata y consistente .
Y i tiene esta propiedad interesante de que si lo cuadramos ( i × i ) obtenemos -1 que está de vuelta a ser un número real. De hecho, esa es la definición correcta:
Número imaginario : Un número cuyo cuadrado es un negativo Número real.
Y i (la raíz cuadrada de -1) por cualquier número real es un número imaginario. Estos son todos los números imaginarios:
- 3 i
- -6 i
- 0,05 i
- π i
También hay muchas aplicaciones para los números imaginarios, por ejemplo en los campos de la electricidad y la electrónica.
Números reales vs imaginarios
Originalmente se reían de los números imaginarios, por lo que obtuvieron el nombre de “imaginario”. Y los números reales obtuvieron su nombre para distinguirlos de los números imaginarios.
Entonces los nombres son solo una cosa histórica. Los números reales no están “en el mundo real” (de hecho, ¡trata de encontrar exactamente la mitad de algo en el mundo real!) Y los números imaginarios no están “solo en la imaginación” … son tipos válidos y útiles de números!
De hecho, a menudo se usan juntos …
“¿y si juntamos un número real y un número imaginario juntos?”
Números complejos
Sí, si juntamos un número real y un número imaginario obtenemos un nuevo tipo de número llamado Número complejo y aquí hay algunos ejemplos:
- 3 + 2 i
- 27,2 – 11,05 i
Un número complejo tiene una parte real y una parte imaginaria, pero cualquiera de los dos podría ser cero
Entonces, un número real es también un número complejo (con una parte imaginaria de 0):
- 4 es un número complejo (porque es 4 + 0 i )
y del mismo modo, un número imaginario es también un número complejo (con una parte real de 0):
- 7 i es un número complejo (porque es 0 + 7 i )
Por lo tanto, los números complejos incluyen todos los números reales y todos los números imaginarios, y todas sus combinaciones.
¡Y eso es todo!
Esos son todos los tipos de números más importantes en matemáticas.
Desde los números de conteo hasta los números complejos.
Hay otros tipos de números, porque las matemáticas son un tema amplio, pero eso debería ayudarte por ahora.
Resumen
Aquí están de nuevo:
| Tipo de número | Descripción rápida |
|---|---|
| Contar números | {1, 2, 3, …} |
| Números enteros | {0, 1, 2, 3, …} |
| Enteros | {…, -3, -2, -1, 0, 1, 2, 3, …} |
| Números racionales | p / q: pyq son enteros, q no es cero |
| Números irracionales | No racional |
| Números reales | Racionales e irracionales |
| Números imaginarios | Cuadrarlos les da un número real negativo |
| Números complejos | Combinaciones de números reales e imaginarios |
Notas finales
Historia
La historia de las matemáticas es muy amplia, con diferentes culturas (griegos, romanos, árabes, chinos, indios y europeos) siguiendo diferentes caminos, y muchas afirmaciones de “¡pensamos en ello primero!” , pero el orden general de descubrimiento que discutí aquí da una buena idea de ello.
Preguntas
¿Y no es sorprendente cuántas veces eso hace una pregunta, como
- “qué sucede si contamos hacia atrás hasta cero” o
- “¿Cuál es la distancia exacta a través de la diagonal del cuadrado”
primero condujo al desacuerdo (¡e incluso al ridículo!), Pero finalmente a avances asombrosos en la comprensión.
Me pregunto qué preguntas interesantes se hacen ahora.
¡A ti!
Aquí hay dos preguntas que puede hacer cuando aprende algo nuevo:
¿Puede ir para otro lado?
- Los números positivos conducen a números negativos
- Los cuadrados conducen a raíces cuadradas
- etc.
¿Puedo usar esto con algo más que conozco?
- Si las fracciones son números, ¿se pueden sumar, restar, etc.?
- ¿Puedo sacar la raíz cuadrada de un número complejo? (¿puedes?)
- etc.
¡Y un día tus preguntas pueden conducir a un nuevo descubrimiento!
