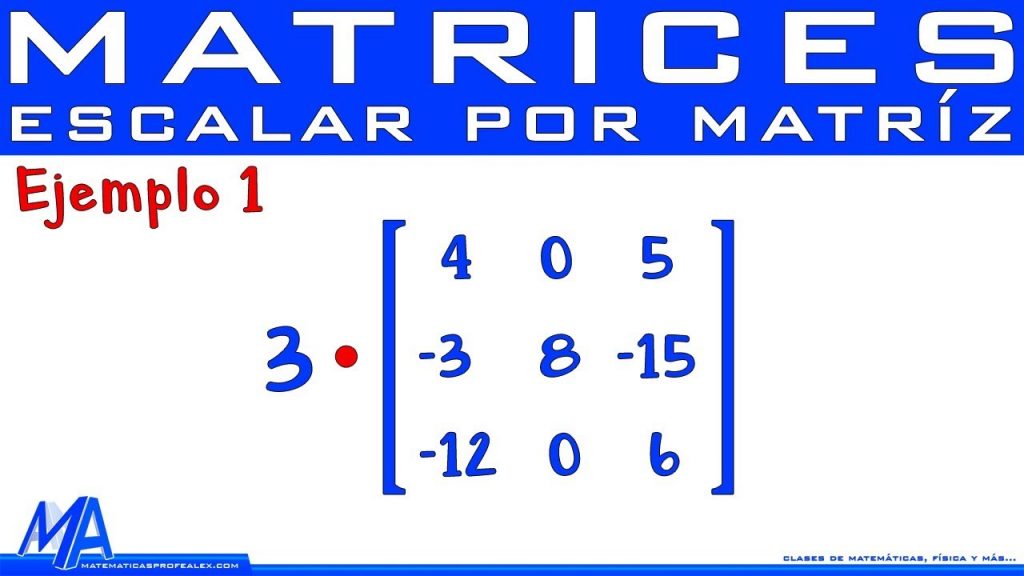
reglas para multiplicar matrices
Nos preguntamos entonces para cuales primos se tiene que el anillo es un cuerpo. El anillo con las operaciones anteriormente descritas será denotado indiferentemente como o . Aunque podría pensarse que los anillos y construidos anteriormente son distintos, puede verse de forma fácil que ellos son algebraicamente iguales, o sea, son isomorfos. En efecto, basta considerar la función → definida por , para todo .
Para hacer el producto y el cociente de dos matrices elemento a elemento, es requisito que ambas tengan la misma dimensión. La matriz final se consigue multiplicando o dividiendo los elementos que llenan exactamente el mismo sitio en ambas matrices. Recuerde que sólo se tienen la posibilidad de producir matrices triangulares a partir de matrices cuadradas. En las matrices triangulares inferiores los elementos que están por encima de la diagonal principal son nulos y en las matrices triangulares superiores lo son los que están abajo, los restantes elementos coinciden con los de la matriz de partida. Hay que tener en cuenta que las funcionalidades exp, log y sqrt se aplican a cada uno de los elementos de la matriz. La función diag genera un vector columna que tiene dentro los elementos de la diagonal principal de la matriz. Obsérvese que como Gretl no dispone de espacio bastante para mostrar las 10 columnas que forman la matriz traspuesta, emplea 2 líneas para mostrar cada fila de la matriz.
Matemáticas Ii Tema 1: Matrices Y Determinantes
Si bien y no sean cero, su producto si puede serlo. Es decir, aunque existan los dos y , estos no tienen por qué razón coincidir. Más allá de que la definición que hemos proporcionado del producto tiene sentido desde una perspectiva un poco más abstracta, deseamos poder calcular explícitamente el producto sabiendo las entradas de y de .
Tienes que rememorar de memoria todas y cada una de las combinaciones para todos y cada uno de los números e incluso si bien las supieses en el momento en que tenías 10 años, recordarlas en este momento sin cometer fallos puede ser una ardua labor. De ahí que, para guiarte a rememorar las tablas de multiplicar del 6, 7, 8 y 9, que son las más bien difíciles por el hecho de que emplean números más grandes, te vamos a contar unos cuantos truquitos. En la situacion de una suma de fracciones, debes encontrar el denominador común, y la forma más fácil es multiplicar las dos cifras de cada fracción por el denominador de la otra para que tengan el mismo denominador. En lugar de sacar tu móvil o tener que recordar las tablas de multiplicar realizando la operación en un papel, ahora te desvelamos de qué forma calcular la multiplicación de números altos de cabeza. Bien, para pasar los grados Celsius a Fahrenheit, tienes que multiplicar la temperatura por 2 y sumarle 30.
Características à permite ver algunas “características” o peculiaridades de la matriz. Las “propiedades” varian dependiendo del tipo de matriz. De esta forma, para matrices cuadradas, aparte de informar de su dimensión, rango y norma, proporciona la traza, el esencial, los valores propios, si es simétrica, si es definida efectiva y si es idempotente. Si “A” es una matriz cuadrada (el número de renglones y columnas es el mismo), su determinante es un valor numérico que se calcula con todos y cada uno de los coeficientes de la matriz. Las reglas para potencias de los números reales asimismo son aplicadas a la capacidad de una matriz, o sea, si una matriz está elevada a una capacidad, solo basta multiplicar exactamente la misma matriz el número de ocasiones que marca la capacidad. El tema posterior a las reglas de los signos es la división de números con signos. En los siguientes temas que versan sobre operaciones algebraicas y sistemas de ecuaciones se necesita la utilización de dichas reglas.
reglas para multiplicar matrices
Esto fue efectuado adecuadamente por 6 de los 9 alumnos. Otra situación de validación está en la segunda actividad de el papel de trabajo, en donde se les solicitó a los estudiantes que escribieran de manera simbólica la relación que se cumplía entre los lados de los rectángulos y el área de dicha figura . Esta representación simbólica es un aspecto esencial en la situación didáctica de institucionalización.
- Este viernes, el conjunto de mujeres se reunió para mostrar su negocio como una parte del concurso que lanzó la Secretaría de Avance y también Integración Social para premiar los proyectos que generaran mayor número de ganancias con el recurso otorgado.
- En este trabajo de investigación se presentó una propuesta didáctica, que orienta al estudiante a conjeturar las reglas de los signos a través de una situación inconveniente.
También describieron las condiciones que deben cumplir los movimientos para llegar a Cataña y la relación con el área sombreada . El repertorio lingüístico y simbólico es el que plasman los alumnos en sus respectivas hojas de trabajo. Asimismo el estudiante podía transitar entre las ocupaciones del software y las hojas de trabajo reconstruyendo sus apreciaciones . La propuesta didáctica fue aplicada a 9 estudiantes del segundo nivel de secundaria de edades entre 12 a 16 años. Se escogió 20% de la población de estudio de cada escuela participante. Esta última actividad da la pauta para saber si el estudiante expone la representación simbólica de las reglas de los signos.
Lea mas sobre bolsa-termica.com aqui.
Los números de Fibonacci aparecen habitualmente en la naturaleza, eminentemente en la botánica, donde a su presencia se le conoce como la ley de Ludwig. Por ejemplo, en las margaritas están 21 espirales en sentido de las manecillas del reloj y 34 en contra; otras relaciones que se han encontrado son 1-2 , 1-3 , 2-5 , 3-8 , 5-13 , 8-13 (piña), etcétera.
Lea mas sobre descargarplusdede.com aqui.
Y se mostró porqué los números complejos tienen la posibilidad de escribirse como . En la actualidad, la primera noción de número complejo que se presenta a un estudiante, radica en definir el conjunto , donde la suma se hace ingrediente a componente y el producto se define como , para todo . Con esto se prueba que el conjunto tiene estructura de cuerpo. En cursos más avanzados de álgebra los complejos se ven como el anillo cociente o asimismo como el grupo de matrices cuadradas , con las operaciones usuales .
La función eigengen permite calcular y almacenar las raíces y vectores propios de una matriz cuadrada. Para almacenar los vectores propios es requisito hacerlo en una matriz que haya sido definida antes. Recuerde que una matriz identidad es una matriz cuadrada con elementos diagonales iguales a uno y elementos no diagonales nulos. Recuerde que el esencial sólo esta definido para matrices cuadradas. Nombrar nuevamente à permite cambiar el nombre de la matriz. Debe tenerse presente que cuando se renombra una matriz esta deja de existir con el nombre antiguo y pasa a estar disponible bajo la novedosa denominación. Ver à deja visualizar el contenido de la matriz e informa de su dimensión.
La página 1 presenta brevemente la historia del secuestro de la princesa y de la encomienda que hace el rey al caballero Ham para ir en su salve. En la página 2 se pide al estudiante abrir el archivo diseñado en el software Cabri y asistir al caballero a rescatar a la princesa.
