
Actividad: un experimento con un dado
|
Necesitarás:
|
 |
Punto interesante
Muchas personas piensan que uno de estos cubos se llama “un dado”. ¡Pero no!
El plural es dado , pero el singular es dado . (es decir, 1 dado, 2 dados).
El dado común tiene seis caras:
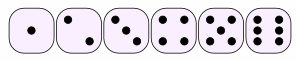
Generalmente llamamos a las caras 1, 2, 3, 4, 5 y 6.
Alto, bajo y más probable
Antes de comenzar, pensemos en lo que podría suceder.
Pregunta: Si tira un dado:
- 1. ¿Cuál es el puntaje mínimo posible?
- 2. ¿Cuál es el puntaje mayor posible?
- 3. ¿Cuál cree que es el puntaje más probable ?
Las dos primeras preguntas son bastante fáciles de responder:
- 1. La puntuación menos posible debe ser 1
- 2. El mayor puntaje posible debe ser 6
- 3. La puntuación más probable es … ???
¿Son todos tan probables? ¿O pasarán algunas más a menudo?
Veamos cuál es más probable …
El experimento
Lanza un dado 60 veces,
registra las puntuaciones en una tabla de conteo.
Puede registrar los resultados en esta tabla usando marcas de conteo :
| Puntuación | Tally | Frecuencia |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| Frecuencia total = | 60 |
OK, ¡vete!
… …
… …
… …

Terminado …?
Ahora dibuja un gráfico de barras para ilustrar tus resultados.
Puedes hacer el tuyo.
O puede usar Gráficos de datos (barra, línea y pastel) y luego imprimirlo.
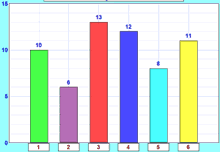
Puede obtener algo como esto:
- ¿Todas las barras tienen la misma altura?
- Si no … ¿por qué no?
60 tiros
OK, ¿por qué te pedí que hicieras 60 tiros? Bueno, 6 lanzamientos no son suficientes para obtener buenos resultados. 600 dará buenos resultados pero es mucho trabajo. Entonces 60 parece estar bien, y también es 10 lotes de 6 .
Entonces deberíamos esperar 10 de cada número, así:
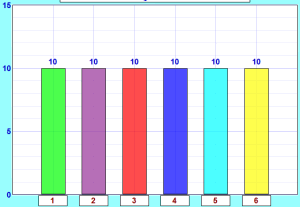
Esos son los valores teóricos ,
¡a diferencia de los experimentales que obtuviste de tu experimento !
¿Cómo se comparan esos resultados teóricos con sus resultados experimentales?
Este gráfico y su gráfico deben ser similares , pero no es probable que sean exactamente iguales, ya que su experimento se basó en la oportunidad , y la cantidad de veces que lo hizo Era bastante pequeño.
Si hicieras el experimento muchas veces, obtendrías resultados mucho más cercanos a los teóricos.
Preguntas
- ¿Qué rostro aparecía con más frecuencia? ____
- ¿Qué rostro aparecía con menos frecuencia? ____
- ¿Crees que obtendrías los mismos resultados si hicieras esto de nuevo? Sí / no
Un experimento da resultados.
Cuando se hace de nuevo, puede dar resultados diferentes.
Por lo tanto, es importante saber cuándo los resultados son de buena calidad , o simplemente al azar .
Probabilidad
En la página Probabilidad encontrará una fórmula:
Probabilidad de que ocurra un evento = Número de formas en que puede suceder Número total de resultados
Ejemplo: probabilidad de un 2
Sabemos que hay 6 resultados posibles.
Y solo hay 1 forma de obtener un 2.
Entonces la probabilidad de obtener 2 es:
Probabilidad de un 2 = 1 6
Hacer eso por cada puntaje nos consigue:
| Puntuación | Probabilidad |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| Total = 1 |
La suma de todas las probabilidades es 1
Para cualquier experimento:
La suma de las probabilidades de todos resultados posibles siempre es igual a 1
