Bases numéricas
Base 10
Utilizamos “Base 10” todos los días … es nuestro Sistema de números decimales .
Tiene 10 dígitos:
1 2 3 4 5 6 7 8 9
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | Entonces 2 | |
| ⋮ | |||
| ••••••••• | 9 | Hasta 9 | |
| •••••••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• • |
11 | ||
| •••••••••• •• |
12 | ||
| ⋮ | |||
| •••••••••• ••••••••• |
19 | ||
| •••••••••• •••••••••• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• •••••••••• • |
21 | ¡Y así sucesivamente! |
¡Pero hay otras bases!
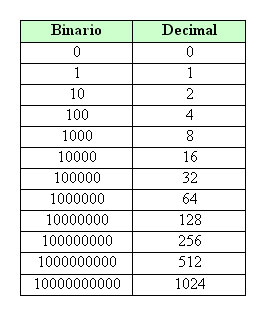
Binario (Base 2) tiene solo 2 dígitos: 0 y 1
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••• | 11 | ||
| •••• | 1 00 | comienza de nuevo en 0 y agrega uno al número de la izquierda … … pero ese número ya está en 1, por lo que también vuelve a 0 … … y 1 se agrega a la siguiente posición a la izquierda |
|
| ••••• | 101 | ||
| •••••• | 110 | ||
| ••••••• | 111 | ||
| •••••••• | 1 000 | Comience nuevamente en 0 (para los 3 dígitos), agregue 1 a la izquierda |
|
| ••••••••• | 1001 | ¡Y así sucesivamente! |
Vea cómo se hace en esta pequeña demostración (presione play):
Prueba también Decimal y otras bases como 3 o 4.
Le ayudará a comprender cómo funcionan todas estas bases diferentes.
Ternary (Base 3) tiene 3 dígitos: 0, 1 y 2
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | ||
| ••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••• | 11 | ||
| ••••• | 12 | ||
| •••••• | 2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••••••• | 21 | ||
| •••••••• | 22 | ||
| ••••••••• | 1 00 | comienza de nuevo en 0 y agrega uno al número de la izquierda … … pero ese número ya está en 2, por lo que también vuelve a 0 … … y 1 se agrega a la siguiente posición a la izquierda |
|
| •••••••••• | 101 | ¡Y así sucesivamente! |
Cuaternario (Base 4) tiene 4 dígitos: 0, 1, 2 y 3
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••••• | 11 | ||
| •••••• | 12 | ||
| ••••••• | 13 | ||
| •••••••• | 2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••••••••• | 21 | ¡Y así sucesivamente! |
Quinario (Base 5) tiene 5 dígitos: 0, 1, 2, 3 y 4
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 4 | ||
| ••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••• | 11 | ||
| ••••••• | 12 | ||
| •••••••• | 13 | ||
| ••••••••• | 14 | ||
| •••••••••• | 2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• • |
21 | ¡Y así sucesivamente! |
Senary (Base 6) tiene 6 dígitos: 0, 1, 2, 3, 4 y 5
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | ||
| ••• | 3 | ||
| •••• | 4 | ||
| ••••• | 5 | ||
| •••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••••••• | 11 | ||
| •••••••• | 12 | ||
| ••••••••• | 13 | ||
| •••••••••• | 14 | ||
| •••••••••• • |
15 | ||
| •••••••••• •• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• ••• |
21 | ¡Y así sucesivamente! |
Septenario (Base 7) tiene 7 dígitos: 0, 1, 2, 3, 4 5 y 6
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | Entonces 2 | |
| ⋮ | |||
| •••••• | 6 | Hasta 6 | |
| ••••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••• | 11 | ||
| ••••••••• | 12 | ||
| ⋮ | |||
| •••••••••• ••• |
16 | ||
| •••••••••• •••• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• ••••• |
21 | ¡Y así sucesivamente! |
Octal (Base 8) tiene 8 dígitos: 0, 1, 2, 3, 4, 5, 6 y 7
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | Entonces 2 | |
| ⋮ | |||
| ••••••• | 7 | Hasta 7 | |
| •••••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| ••••••••• | 11 | ||
| •••••••••• | 12 | ||
| ⋮ | |||
| •••••••••• ••••• |
17 | ||
| •••••••••• •••••• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• ••••••• |
21 | ¡Y así sucesivamente! |
Nonary (Base 9) tiene 9 dígitos: 0, 1, 2, 3, 4, 5, 6, 7 y 8
Contamos así:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | Entonces 2 | |
| ⋮ | |||
| •••••••• | 8 | Hasta 8 | |
| ••••••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• | 11 | ||
| •••••••••• • |
12 | ||
| ⋮ | |||
| •••••••••• ••••••• |
18 | ||
| •••••••••• •••••••• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• ••••••••• |
21 | ¡Y así sucesivamente! |
Decimal (Base 10) tiene 10 dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
Bueno … hablamos de esto al principio pero aquí está de nuevo:
| 0 | Comienza en 0 | ||
| • | 1 | Entonces 1 | |
| •• | 2 | Entonces 2 | |
| ⋮ | |||
| ••••••••• | 9 | Hasta 9 | |
| •••••••••• | 1 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• • |
11 | ||
| •••••••••• •• |
12 | ||
| ⋮ | |||
| •••••••••• ••••••••• |
19 | ||
| •••••••••• •••••••••• |
2 0 | Comienza de nuevo en 0 nuevamente, pero agrega 1 a la izquierda | |
| •••••••••• •••••••••• • |
21 | ¡Y así sucesivamente! |
Indecimal (Base 11)
Undecimal (Base 11) necesita un dígito más que Decimal, por lo que se usa “A”, como esto:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indeciso: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | 10 | 11 | … |
Duodecimal (Base 12)
Duodecimal (Base 12) necesita dos dígitos más que Decimal, por lo que se utilizan “A” y “B”:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Duodecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | 10 | 11 | … |
Hexadecimal (Base 16)
Debido a que hay más de 10 dígitos, el hexadecimal también se escribe con letras, como esta:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hexadecimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | … |
Vigesimal (Base 20)
Con vigesimal, la convención es que I no se usa porque parece 1 , entonces J = 18 y K = 19, como en esta tabla:
| Decimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vigesimal: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | G | H | J | K | 10 | … |
Más sobre bases
Nota: la base numérica también se llama Radix
Cómo mostrar la base
Para mostrar qué base tiene un número, coloca la base en la esquina inferior derecha de esta manera:
101 2
Esto muestra que está en Base 2 (Binario)
314 8
Esto muestra que está en Base 8 (Octal)
