Colorear (Los cuatro colores
Teorema)
Esta actividad se trata de colorear, pero no
creo que es solo cosa de niños. Esta investigación conducirá a uno de los
Teoremas más famosos de las matemáticas y algunos resultados muy interesantes.
¿Alguna vez has coloreado un patrón y
se preguntó cuántos colores necesita usar?
Solo hay una regla
¡Dos secciones que comparten un borde común no pueden tener el mismo color!
Tener una esquina común está bien, pero no una ventaja.
Comencemos con un patrón simple como un grupo
de nueve cuadrados:
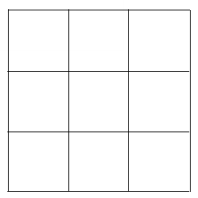
¿Cuántos colores necesitas para colorear el
patrón de nueve cuadrados?
Podría usar nueve colores diferentes, pero
podría conformarse con tan solo dos :

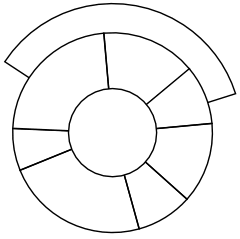
Un poco más complicado
¿Qué tal este?
¿Cuántos colores necesitas esta vez?
Te toca … pruébalo … luego desplázate hacia abajo para ver mi respuesta
…
…
Podría usar cuatro colores diferentes, o podría conformarse con solo
tres :

Pero no podría colorear este patrón con solo dos colores. Puedes ver
¿por qué?
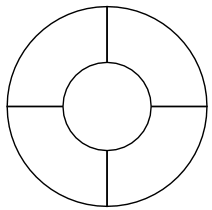
Aún más complicado
Probemos con otro:
¿Cuántos colores necesitas esta vez?
¿Nueve? ¿Ocho? ¿Siete? ¿Seis? ¿Cinco? Cuatro?
Pruébalo tú mismo antes de ver mi respuesta.
…
…
|
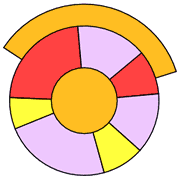
Necesitaba cuatro colores para colorear este patrón. puedo cambiar los colores I |
 |
Mapas
Esto podría ser un poco más interesante si quisiéramos colorear un mapa.
Un mapa puede no funcionar cuando un país tiene dos o más áreas separadas, como Alaska (parte de los Estados Unidos, pero con Canadá en el medio) o Kaliningrado (parte de Rusia, pero tampoco unido). Pero ignoremos eso aquí.
Aquí
es un mapa de parte de Europa, que muestra nueve países y cómo limitan
el uno del otro:
Intenta colorear en el mapa y observa cuál es la menor cantidad de colores que puedes
necesitar.
Nuevamente, ¡no mires mi respuesta hasta que la hayas probado tú mismo!
…
…
Así es como lo hice. Necesitaba usar cuatro
colores:

Cuatro colores
Parece que cualquier
patrón o mapa siempre se puede colorear con cuatro colores .
En algunos casos,
Como en el primer ejemplo, podríamos usar menos de cuatro. En muchos casos pudimos
usar muchos más colores si quisiéramos, pero un máximo de cuatro colores es
suficiente !
Este resultado se ha convertido en uno de los teoremas matemáticos más famosos
y se conoce como Los cuatro colores
Teorema.
Entonces, ¿por qué es importante?
Es importante porque se declaró por primera vez en 1852, pero no se demostró
hasta 1976. Durante más de ciento veinte años, algunos de los mejores
cerebros matemáticos en el mundo no tuvieron éxito en probar uno de
Los teoremas más simples de las matemáticas. Había muchas pruebas falsas, y
se desarrolló una nueva rama de las matemáticas, conocida como Graph Theory , para intentar
para resolver el teorema Pero nadie pudo probarlo hasta que en 1976 Appel y
Haken demostró el teorema con la ayuda de una computadora.
Algunas personas piensan
que, aunque su prueba era correcta, era una trampa usar un
computadora. ¿Qué piensas?
¡Se puede cambiar un mapa!
Ahora mira nuevamente nuestros dos ejemplos anteriores:

¿Puedes ver la similitud entre estos dos diagramas?
Imagine que el mapa de los países europeos se dibujó en una pieza de goma
eso podría estirarse. Al estirar y torcer la pieza de goma
de cierta manera, podrías terminar con el diagrama circular.
Decimos que son homeomórficos.
Esa es una gran palabra, pero una idea muy simple: uno puede convertirse en el otro .
También forma parte
de una gran rama de las matemáticas conocida como Topología.
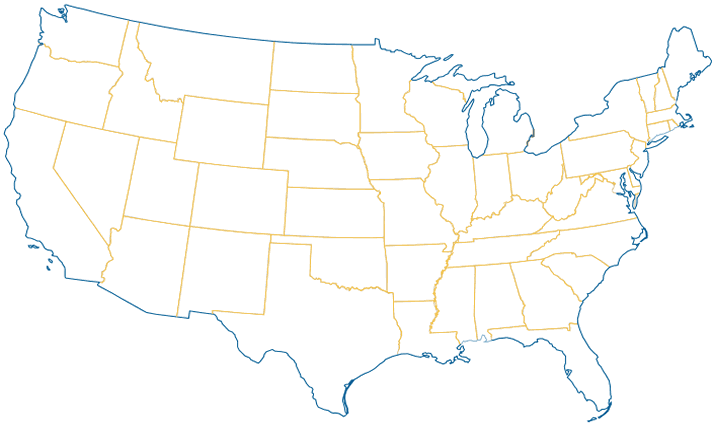
Uno más: Estados Unidos
Aquí hay uno para que pruebes por tu cuenta … los “contiguos” (es decir, todos conmovedores) Estados Unidos (sin Alaska ni Hawai).
¿Puedes colorearlo usando solo 4 colores?