
Completando la plaza
“ Completando el cuadrado ” es donde nosotros …
| … tome una Ecuación cuadrática así: |
|
y gírelo en esto: |
| hacha 2 + bx + c = 0 | a (x + d ) 2 + e = 0 |
Pero si tienes tiempo, déjame mostrarte cómo “ Completa el cuadrado ” tú mismo.
Completando la plaza
Digamos que tenemos una expresión simple como x 2 + bx . Tener x dos veces en la misma expresión puede dificultar la vida. ¿Qué podemos hacer?
Bueno, con un poco de inspiración de Geometry podemos convertirlo, así:
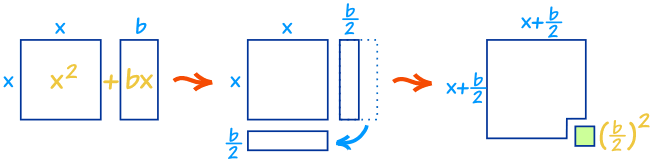
Como puede ver x 2 + bx se puede reorganizar casi en un cuadrado …
… y podemos completar el cuadrado con (b / 2) 2
En álgebra se ve así:
| x 2 + bx | + (b / 2) 2 | = | (x + b / 2) 2 |
| “Completa el cuadrado” |
Entonces, agregando (b / 2) 2 podemos completar el cuadrado.
Y (x + b / 2) 2 tiene x solo una vez , que es más fácil de usar.
Manteniendo el equilibrio
Ahora … no podemos simplemente agregar (b / 2) 2 sin también [19459004 ] restando también! De lo contrario, todo el valor cambia.
Entonces, veamos cómo hacerlo correctamente con un ejemplo:
| Comience con: | |
| (“b” es 6 en este caso) | |
| Completa el cuadrado: | |
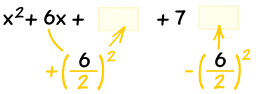 También resta el nuevo término |
|
|
Simplifícalo y listo. |
|
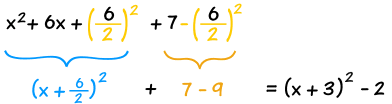 |
|
El resultado:
x 2 + 6x + 7 = (x + 3) 2 – 2
Y ahora x solo aparece una vez, ¡y nuestro trabajo está hecho!
Un enfoque de acceso directo
Aquí hay una forma rápida de obtener una respuesta. Te puede gustar este método.
Primero piense en el resultado que queremos: (x + d) 2 + e
Después de expandirse (x + d) 2 obtenemos: x 2 + 2dx + d 2 + e
Ahora ve si podemos convertir nuestro ejemplo en esa forma para descubrir d y e
Ejemplo: intente ajustar x 2 + 6x + 7 en x 2 + 2dx + d 2 + e
![x^2 + (6x) + [7] matches x^2 + (2dx) + [d^2+e]](https://www.mathsisfun.com/algebra/images/completing-square-expanded.gif)
Ahora podemos “forzar” una respuesta:
- Sabemos que 6x debe terminar como 2dx , entonces d debe ser 3 [19459061 ]
- Luego vemos que 7 debe convertirse en d 2 + e = 9 + e , entonces e ] debe ser −2
¡Y obtenemos el mismo resultado (x + 3) 2 – 2 como arriba!
Ahora, veamos una aplicación útil: resolver ecuaciones cuadráticas …
Resolviendo ecuaciones cuadráticas generales completando el cuadrado
Podemos completar el cuadrado para resolver a Ecuación cuadrática (encontrar dónde es igual a cero).
Pero una ecuación cuadrática general puede tener un coeficiente de a delante de x 2 :
hacha 2 + bx + c = 0
Pero eso es fácil de tratar … solo divide la ecuación completa por “a” primero, luego continúa:
x 2 + (b / a) x + c / a = 0
Pasos
Ahora podemos resolver una ecuación cuadrática en 5 pasos:
- Paso 1 Divida todos los términos entre a (el coeficiente de x 2 ).
- Paso 2 Mueva el término numérico ( c / a ) al lado derecho de la ecuación.
- Paso 3 Completa el cuadrado en el lado izquierdo de la ecuación y equilibra esto agregando el mismo valor al lado derecho de la ecuación.
Ahora tenemos algo parecido a (x + p) 2 = q, que se puede resolver con bastante facilidad:
- Paso 4 Saca la raíz cuadrada a ambos lados de la ecuación.
- Paso 5 Resta el número que queda en el lado izquierdo de la ecuación para encontrar x .
Ejemplos
OK, ¡algunos ejemplos ayudarán!
Ejemplo 1: Resolver x 2 + 4x + 1 = 0
El paso 1 se puede omitir en este ejemplo ya que el coeficiente de x 2 es 1
Paso 2 Mueva el término numérico al lado derecho de la ecuación:
Paso 3 Completa el cuadrado en el lado izquierdo de la ecuación y equilibra esto agregando el mismo número al lado derecho de la ecuación.
(b / 2) 2 = (4/2) 2 = 2 2 = 4
Paso 4 Saca la raíz cuadrada a ambos lados de la ecuación:
Paso 5 Resta 2 de ambos lados:
|
Y aquí hay algo interesante y útil.
Al final del paso 3 teníamos la ecuación:
(x + 2 ) 2 = 3
Nos da el vértice (punto de inflexión) de x 2 + 4x + 1: (-2, -3) [19459015 ] |
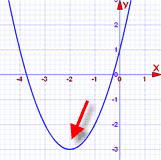 |
Ejemplo 2: resolver 5x 2 – 4x – 2 = 0
Paso 1 Divide todos los términos entre 5
Paso 2 Mueva el término numérico al lado derecho de la ecuación:
Paso 3 Completa el cuadrado en el lado izquierdo de la ecuación y equilibra esto agregando el mismo número al lado derecho de la ecuación:
(b / 2) 2 = (0.8 / 2) 2 = 0.4 2 = 0.16
Paso 4 Saca la raíz cuadrada a ambos lados de la ecuación:
Paso 5 Reste (-0.4) de ambos lados (en otras palabras, agregue 0.4):
¿Por qué “completar el cuadrado”?
¿Por qué completar el cuadrado cuando solo podemos usar la Fórmula cuadrática para resolver una ecuación cuadrática?
Bueno, una razón se da arriba, donde la nueva forma no solo nos muestra el vértice, sino que hace que sea más fácil de resolver.
También hay momentos en que la forma ax 2 + bx + c puede ser parte de una mayor pregunta y reorganizarla como a ( x + d ) 2 + e hace la solución más fácil, porque x solo aparece una vez.
Por ejemplo, “x” puede ser una función en sí misma (como cos (z) ) y reorganizarla puede abrir un camino hacia una mejor solución.
También completar el cuadrado es el primer paso en la Derivación de la fórmula cuadrática
Solo piense en ello como otra herramienta en su caja de herramientas de matemáticas.
Nota al pie: valores de “d” y “e”
¿Cómo obtuve los valores de d y e desde la parte superior de la página?
| Comience con | |
| Divida la ecuación por a | |
| Coloque c / a en el otro lado | |
| Agregue (b / 2a) 2 a ambos lados | |
| “Completa el cuadrado” | |
| Ahora trae todo de vuelta … | |
| … al lado izquierdo | |
| … al múltiplo original a de x 2 | |
b
2a
b 2
4a
