
Cuadrática de factorización

Una ecuación cuadrática en forma estándar
( a , b y c pueden tener cualquier valor, excepto que a no puede ser 0.) [ 19459010]
Para “Factorizar” (o “Factorizar” en el Reino Unido) una Cuadrática es:
encuentra qué multiplicar para obtener el Cuadrático
Se llama “Factoring” porque encontramos los factores (un factor es algo por lo que multiplicamos)
Ejemplo:
Multiplicando (x + 4) y (x − 1) juntos (llamado Expandiendo ) obtiene x 2 + 3x – 4 :

Entonces (x + 4) y (x − 1) son factores de x 2 + 3x – 4 [19459012 ]
Solo para estar seguros, verifiquemos:

Sí, (x + 4) y (x − 1) son definitivamente factores de x 2 + 3x – 4
¿Viste que Expandir y Factorizar son opuestos?

La expansión suele ser fácil, pero la factorización a menudo puede ser complicada .
Es como tratar de encontrar qué ingredientes
entró en un pastel para hacerlo tan delicioso.
¡Puede ser difícil de entender!
Así que intentemos un ejemplo en el que aún no conozcamos los factores:
Factor común
Primero verifique si hay factores comunes.
Ejemplo: ¿cuáles son los factores de 6x 2 – 2x = 0 ?
6 y 2 tienen un factor común de 2 :
2 (3x 2 – x) = 0
Y x 2 y x tienen un factor común de x :
2x (3x – 1) = 0
¡Y lo hemos logrado! Los factores son 2x y 3x – 1 ,
Ahora también podemos encontrar las raíces (donde es igual a cero):
- 2x es 0 cuando x = 0
- 3x – 1 es cero cuando x = 1 3
Y este es el gráfico (vea cómo es cero en x = 0 yx = 1 3 ):
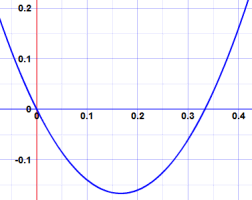
Pero no siempre es tan fácil …
Adivina y verifica
¿Quizás podamos adivinar una respuesta?
Ejemplo: ¿cuáles son los factores de 2x 2 + 7x + 3 ?
No hay factores comunes.
Intentemos adivinar una respuesta, y luego verifiquemos si tenemos razón … ¡podríamos tener suerte!
Podríamos adivinar (2x + 3) (x + 1):
(2x + 3) (x + 1) = 2x 2 + 2x + 3x + 3
= 2x 2 + 5x + 3 (INCORRECTO)
¿Qué tal (2x + 7) (x − 1):
(2x + 7) (x − 1) = 2x 2 – 2x + 7x – 7
= 2x 2 + 5x – 7 (OTRA VEZ MAL)
OK, ¿qué tal (2x + 9) (x − 1):
(2x + 9) (x − 1) = 2x 2 – 2x + 9x – 9
= 2x 2 + 7x – 9 (OTRA VEZ MAL)
¡Oh, no! Podríamos estar adivinando durante mucho tiempo antes de tener suerte.
Ese no es un muy buen método. Así que intentemos algo más.
Un método para casos simples
Afortunadamente hay un método que funciona en casos simples.
Con la ecuación cuadrática en esta forma:

Paso 1 : Encuentra dos números que se multiplican para dar ac (en otras palabras, a veces c), y suma para dar b .
Ejemplo: 2x 2 + 7x + 3
ac es 2 × 3 = 6 yb es 7
Entonces, queremos dos números que se multipliquen para formar 6 y sumen 7
De hecho 6 y 1 hacen eso (6 × 1 = 6, y 6 + 1 = 7)
¿Cómo encontramos 6 y 1?
Ayuda enumerar los factores de ac = 6 , y luego intenta agregar algunos para obtener b = 7 .
Los factores de 6 incluyen 1, 2, 3 y 6.
¡Ajá! 1 y 6 suman a 7, y 6 × 1 = 6.
Paso 2 : Reescribe el medio con esos números:
Reescribe 7x con 6 x y 1 x:
2x 2 + 6x + x + 3
Paso 3 : Factoriza los dos primeros y los dos últimos términos por separado:
Los primeros dos términos 2x 2 + 6x factorizan en 2x (x + 3)
Los dos últimos términos x + 3 en realidad no cambian en este caso
Entonces obtenemos:
2x (x + 3) + (x + 3)
Paso 4 : Si lo hemos hecho correctamente, nuestros dos nuevos términos deberían tener un factor común claramente visible.
En este caso podemos ver que (x + 3) es común a ambos términos, por lo que podemos ir:
¡Listo!
Comprobar: (2x + 1) (x + 3) = 2x 2 + 6x + x + 3 = 2x 2 + 7x + 3 ( Sí)
¡Mucho mejor que adivinar!
Veamos los pasos 1 a 4 nuevamente, de una vez :
| 2x 2 + 7x + 3 |
| 2x 2 + 6x + x + 3 |
| 2x (x + 3) + (x + 3) |
| 2x (x + 3) + 1 (x + 3) |
| (2x + 1) (x + 3) |
OK, intentemos con otro ejemplo:
Ejemplo: 6x 2 + 5x – 6
Paso 1 : ac es 6 × (−6) = −36 , yb es 5
Enumere los factores positivos de ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36
Uno de los números tiene que ser negativo para hacer −36, así que al jugar con algunos números diferentes encuentro que −4 y 9 funcionan bien:
−4 × 9 = −36 y −4 + 9 = 5
Paso 2 : Reescribe 5x con −4x y 9x:
6x 2 – 4x + 9x – 6
Paso 3 : Factoriza los dos primeros y los dos últimos:
2x (3x – 2) + 3 (3x – 2)
Paso 4 : El factor común es (3x – 2):
(2x + 3) (3x – 2)
Verificación: (2x + 3) (3x – 2) = 6x 2 – 4x + 9x – 6 = 6x 2 + 5x – 6 ( Sí)
Encontrando esos números
La parte más difícil es encontrar dos números que se multiplican para dar ac , y suman para dar b .
Es en parte una conjetura, y ayuda a enumerar todos los factores .
Aquí hay otro ejemplo para ayudarlo:
Ejemplo: ac = −120 yb = 7
¿Qué dos números se multiplican por −120 y se suman a 7 ?
Los factores de 120 son (más y menos):
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 y 120
Podemos probar pares de factores (¡comenzar cerca del medio!) Y ver si suman 7:
- −10 x 12 = −120 y −10 + 12 = 2 (no)
- −8 x 15 = −120 y −8 + 15 = 7 (¡SÍ!)
Practica un poco
Puede practicar factorización cuadrática simple .
¿Por qué factorizar?
Bueno, uno de los grandes beneficios de la factorización es que podemos encontrar las raíces de la ecuación cuadrática (donde la ecuación es cero).
Todo lo que tenemos que hacer (después de factorizar) es encontrar dónde cada uno de los dos factores se convierte en cero
Ejemplo: ¿cuáles son las raíces (ceros) de 6x 2 + 5x – 6 ?
Ya sabemos (de arriba) los factores son
(2x + 3) (3x – 2)
Y podemos descubrir que
(2x + 3) es cero cuando x = −3/2
y
(3x – 2) es cero cuando x = 2/3
Entonces, las raíces de 6x 2 + 5x – 6 son:
−3/2 y 2/3
Aquí hay una gráfica de 6x 2 + 5x – 6 , ¿puedes ver dónde es igual a cero?

Y también podemos verificarlo con un poco de aritmética:
En x = -3/2 : 6 (-3/2) 2 + 5 (-3/2) – 6 = 6 × (9/4) – 15/2 – 6 = 54/4 – 15/2 – 6 = 6-6 = 0
En x = 2/3 : 6 (2/3) 2 + 5 (2/3) – 6 = 6 × (4/9) + 10/3 – 6 = 24/9 + 10/3 – 6 = 6-6 = 0
Gráficos
También podemos intentar graficando la ecuación cuadrática . Ver dónde es igual a cero puede darnos pistas.
Ejemplo: (continuación)
Comenzando con 6x 2 + 5x – 6 y solo esta trama:

Las raíces son alrededor de x = −1.5 yx = +0.67, por lo que podemos adivinar las raíces son:
−3/2 y 2/3
Lo que puede ayudarnos a resolver los factores 2x + 3 y 3x – 2
¡Siempre revisa sin embargo! El valor del gráfico de +0.67 podría no ser realmente 2/3
La solución general
También hay una solución general (útil cuando falla el método anterior), que utiliza la fórmula cuadrática :

Use esa fórmula para obtener las dos respuestas x + y x – (una es para el caso “+”, y el otro es para el caso “-” en el “±”), y obtenemos este factorización:
a (x – x + ) (x – x – )
Usemos el ejemplo anterior para ver cómo funciona:
Ejemplo: ¿cuáles son las raíces de 6x 2 + 5x – 6 ?
Sustituye a = 6, b = 5 y c = −6 en la fórmula:
x = −b ± √ (b 2 – 4ac) 2a
= −5 ± √ (5 2 – 4 × 6 × (−6)) 2 × 6 [19459012 ]
= −5 ± √ (25 + 144) 12
= −5 ± √169 12
= −5 ± 13 12
Entonces las dos raíces son:
x + = (−5 + 13) / 12 = 8/12 = 2/3,
x – = (−5 – 13) / 12 = −18/12 = −3/2
(Observe que obtenemos la misma respuesta que cuando hicimos la factorización antes).
Ahora ponga esos valores en a (x – x + ) (x – x – ) :
6 (x – 2/3) (x + 3/2)
Podemos reorganizar eso un poco para simplificarlo:
3 (x – 2/3) × 2 (x + 3/2) = (3x – 2) (2x + 3)
Y obtenemos los mismos factores que antes.
(Gracias a “mathsyperson” por partes de este artículo)
