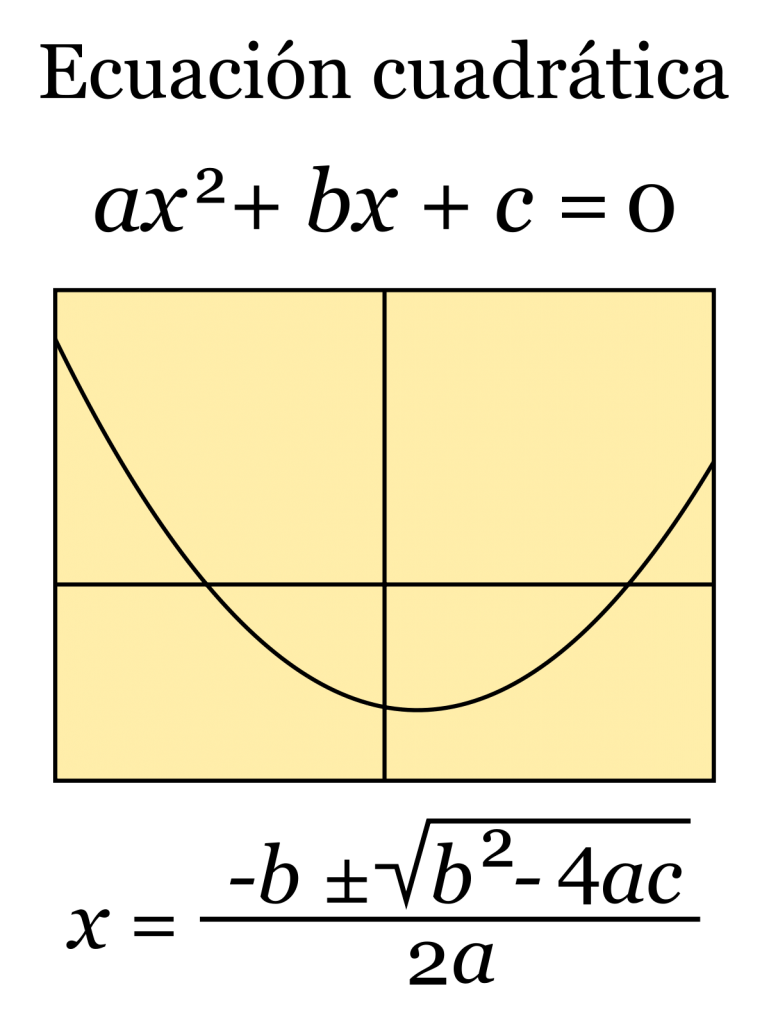
Ecuaciones cuadráticas
Un ejemplo de una Ecuación cuadrática :

Las ecuaciones cuadráticas hacen buenas curvas, como esta:
Nombre
El nombre Cuadrático proviene de “quad” que significa cuadrado, porque la variable obtiene al cuadrado (como x 2 ).
También se llama “Ecuación de Grado 2” (debido al “2” en x )
Formulario estándar
La forma estándar de una ecuación cuadrática se ve así:
- a , b y c son valores conocidos. a no puede ser 0.
- “ x ” es la variable o desconocida (aún no lo sabemos).
Estos son algunos ejemplos:
| 2x 2 + 5x + 3 = 0 | En este a = 2 , b = 5 y c = 3 | |
| x 2 – 3x = 0 | Este es un poco más complicado:
|
|
| 5x – 3 = 0 | ¡Vaya! Esta es no una ecuación cuadrática: falta x 2 (en otras palabras a = 0 , lo que significa que no puede ser cuadrático) |

Juega con él
Juega con el ” Explorador de ecuaciones cuadráticas ” para que puedas ver:
- el gráfico que hace, y
- las soluciones (llamadas “raíces”).
¡Ecuaciones cuadráticas ocultas!
Como vimos antes, la Forma estándar de una ecuación cuadrática es
hacha 2 + bx + c = 0
¡Pero a veces una ecuación cuadrática no se ve así!
Por ejemplo:
| Disfrazado | |
En forma estándar | a, byc |
|---|---|---|---|
| x 2 = 3x – 1 | Mover todos los términos al lado izquierdo | x 2 – 3x + 1 = 0 | a = 1, b = −3, c = 1 |
| 2 (w 2 – 2w) = 5 | Expandir (deshacer los corchetes ), y mueve 5 a la izquierda |
2w 2 – 4w – 5 = 0 | a = 2, b = −4, c = −5 |
| z (z − 1) = 3 | Expande y mueve 3 a la izquierda | z 2 – z – 3 = 0 | a = 1, b = −1, c = −3 |
¿Cómo resolverlos?
Las “ soluciones ” a la ecuación cuadrática son donde está igual a cero .
También se les llama “ raíces “, o a veces “ ceros ”

Generalmente hay 2 soluciones (como se muestra en este gráfico).
Y hay algunas formas diferentes de encontrar las soluciones:
![Quadratic Formula: x = [ -b (+-) sqrt(b^2 - 4ac) ] / 2a](https://www.mathsisfun.com/algebra/images/quadratic-formula.svg)
Simplemente conecte los valores de a, byc, y haga los cálculos.
Veremos este método con más detalle ahora.
Acerca de la fórmula cuadrática
Más / Menos
En primer lugar, ¿qué es esa cosa más / menos que se parece a ± ?
El ± significa que hay DOS respuestas:
x = −b + √ (b 2 – 4ac) 2a
x = −b – √ (b 2 – 4ac) 2a
Aquí hay un ejemplo con dos respuestas:

¡Pero no siempre funciona así!
- Imagine si la curva “solo toca” el eje x.
- O imagina que la curva es tan alta que ni siquiera cruza el eje x.
Aquí es donde el “Discriminante” nos ayuda …
Discriminante
¿Ve b 2 – 4ac en la fórmula anterior? Se llama Discriminante , porque puede “discriminar” entre los posibles tipos de respuesta:
- cuando b 2 – 4ac es positivo, obtenemos dos soluciones Real
- cuando es cero obtenemos UNA sola solución real (ambas respuestas son iguales)
- cuando es negativo obtenemos un par de soluciones Complejo
¿Soluciones complejas? Hablemos de ellos después de ver cómo usar la fórmula.
Usando la fórmula cuadrática
Simplemente pon los valores de a, byc en la Fórmula Cuadrática, y haz los cálculos.
Ejemplo: resolver 5x 2 + 6x + 1 = 0
−b ± √ (b 2 – 4ac)
2a
−6 ± √ (6 2 – 4 × 5 × 1)
2 × 5
−6 ± √ (36 – 20)
10
−6 ± √ (16)
10
−6 ± 4
10
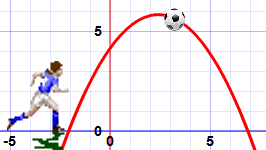
Respuesta: x = −0,2 o x = −1
Y los vemos en este gráfico.
| Verifique -0,2 : | 5 × ( −0,2 ) 2 + 6 × ( −0,2 ) + 1 = 5 × (0.04) + 6 × (−0.2) + 1 = 0,2 – 1,2 + 1 = 0 |
|
| Verifique -1 : | 5 × ( −1 ) 2 + 6 × ( −1 ) + 1 = 5 × (1) + 6 × (−1) + 1 = 5 – 6 + 1 = 0 |
Recordando la fórmula
Un amable lector sugirió cantarlo a “Pop Goes the Weasel”:
| ♫ | “x es igual a menos b | ♫ | “Todo alrededor del arbusto de morera | |
| más o menos la raíz cuadrada | El mono persiguió a la comadreja | |||
| de b-cuadrado menos cuatro a c | El mono pensó que “todo fue divertido” | |||
| TODOS sobre dos a “ | ¡Pop! va la comadreja “ |
¡Intenta cantarlo varias veces y se te quedará atrapado en la cabeza!
O puedes recordar esta historia:
x =
−b ± √ (b 2 – 4ac)
2a
“Un niño negativo estaba pensando sí o no en ir a una fiesta,
en la fiesta habló con un chico cuadrado pero no con las 4 chicas increíbles.
Todo terminó a las 2 de la mañana. “
¿Soluciones complejas?
Cuando el Discriminante (el valor b 2 – 4ac ) es negativo obtenemos un par de soluciones Complejo … ¿qué significa eso?
Significa que nuestra respuesta incluirá Números imaginarios . ¡Guauu!
Ejemplo: resolver 5x 2 + 2x + 1 = 0
= −16
−2 ± √ (−16)
10
√ (−16)
= 4 i
(donde i es el número imaginario √ − 1)
−2 ± 4 i
10
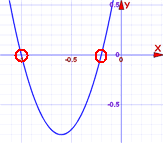
Respuesta: x = −0,2 ± 0,4 i
El gráfico no cruza el eje x. Es por eso que terminamos con números complejos.
De alguna manera es más fácil: no necesitamos más cálculos, simplemente déjelo como −0.2 ± 0.4 i .
Ejemplo: Resolver x 2 – 4x + 6.25 = 0
= −9
√ (−9) = 3 i
(donde i es el número imaginario √ − 1)

Respuesta: x = 2 ± 1,5 i
El gráfico no cruza el eje x. Es por eso que terminamos con números complejos.

PERO una imagen invertida invertida de nuestra ecuación cruza el eje x en 2 ± 1.5 (nota: falta el i ).
¡Solo un hecho interesante para ti!
Resumen
- Ecuación cuadrática en forma estándar: ax 2 + bx + c = 0
- Las ecuaciones cuadráticas se pueden factorizar
- Fórmula cuadrática: x =
−b ± √ (b 2 – 4ac)
2a
- Cuando el discriminante ( b 2 −4ac ) es:
- positivo, hay 2 soluciones reales
- cero, hay una solución real
- negativo, hay 2 soluciones complejas
(Preguntas difíciles: 1 2 3 4 5 6 [ 19459109] 7 8 )

