
enésima raíz
La “enésima raíz” utilizada n veces en una multiplicación da el valor original
“enésimo”
1 st, 2 nd, 3 rd, 4 th, 5 th, .. . n th …
En lugar de hablar del “4to”, “16to”, etc., si queremos hablar en general, decimos el “ n th “.
La enésima raíz
- La raíz “segunda” es la raíz cuadrada
- La raíz “tercera” es la raíz cúbica
- etc.
| 2 | |
Al igual que la raíz cuadrada se usa dos veces en una multiplicación para obtener el valor original. | ||
| 3 | |
Y la raíz cúbica se usa tres veces en una multiplicación para obtener el valor original. | ||
| … | … |
…
|
||
| n | |
La raíz enésima se usa n veces en una multiplicación para obtener el valor original. |
Entonces, es la forma general de hablar sobre las raíces
(por lo que podría ser 2º, 9º, 324º o lo que sea)
El enésimo símbolo raíz
Este es el símbolo especial que significa “enésima raíz”,
es el símbolo “radical” (usado para raíces cuadradas) con un pequeño n que significa enésima raíz.
Utilizándolo
Podríamos usar la enésima raíz en una pregunta como esta:
Pregunta: ¿Qué es “n” en esta ecuación?
Respuesta: Simplemente sé que 625 = 5 4 , por lo que la 4 raíz de 625 debe ser 5:
O podríamos usar “n” porque queremos decir cosas generales:
Ejemplo: cuando n es impar (hablaremos de esto más adelante).
¿Por qué “Root” …?
 |
Cuando veas “root” piensa “Conozco el árbol , pero ¿cuál es la raíz que lo produjo? ” Ejemplo: en √9 = 3 el “árbol” es 9 , y la raíz es 3 . |
Propiedades
Ahora que sabemos qué es una enésima raíz, veamos algunas propiedades:
Multiplicación y división
Podemos “separar” las multiplicaciones bajo el signo raíz de esta manera:
( Si n es par, a y b deben ser ambos ≥ 0)
Esto puede ayudarnos a simplificar las ecuaciones en álgebra y también hacer algunos cálculos más fáciles:
Ejemplo:
También funciona para la división:
( a≥0 yb> 0)
(b no puede ser cero, ya que no podemos dividir por cero)
Ejemplo:
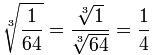
Suma y resta
¡Pero nosotros no podemos hacer ese tipo de cosas para sumas o restas!
| |
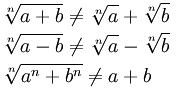 |
|
Ejemplo: Teorema de Pitágoras dice
 |
a 2 + b 2 = c 2 |
Entonces podemos calcular c así:
c = √ (a 2 + b 2 )
¿Cuál es no lo mismo que c = a + b , verdad?
Es una trampa fácil de caer, así que ten cuidado. También significa que, desafortunadamente, las sumas y restas pueden ser difíciles de manejar cuando se está bajo un signo raíz.
Exponentes vs Raíces
Un exponente en un lado de “=” se puede convertir en una raíz en el otro lado de “=”:
| |
Si |
Ejemplo:
enésima raíz de una a la enésima potencia
Cuando un valor tiene un exponente de n y tomamos la enésima raíz nosotros recuperamos el valor nuevamente …
|
… cuando a es positivo (o cero): |
|
 |
(cuando a ≥ 0 ) |
Ejemplo: 
|
… o cuando el exponente es impar : |
|
 |
(cuando n es impar ) |
Ejemplo: 
… pero cuando a es negativo y el exponente es par obtenemos esto:

¿Viste que −3 se convirtió en +3?
| … entonces tenemos: | |
 |
(cuando a <0 y n es par ) |
(Nota: | a | significa el valor absoluto de a, en otras palabras, cualquier negativo se convierte en positivo)
Ejemplo: 
¡Eso es algo de lo que hay que tener cuidado! Lea más en Exponentes de números negativos .
Aquí está en una pequeña mesa:
| n es impar | n es par | |
|---|---|---|
| a ≥ 0 |  |
 |
| a <0 |  |
 |
enésima raíz de a-the-mth-Power
Ahora veamos qué sucede cuando el exponente y la raíz son valores diferentes ( m y n ).
| |
|
Ejemplo:
Entonces … podemos mover el exponente “fuera de” la enésima raíz, lo que a veces puede ser útil.
Pero hay un método aún más potente … podemos combinar el exponente y la raíz para hacer un nuevo exponente, como este:
| |
|
Ejemplo: |
Esto se debe a que la raíz enésima es igual a un exponente de (1 / n) :
| |
|
Ejemplo: 2 ½ = √2 (la raíz cuadrada de 2) |
Te gustaría leer sobre Exponentes fraccionales a continuación para descubrir por qué.
