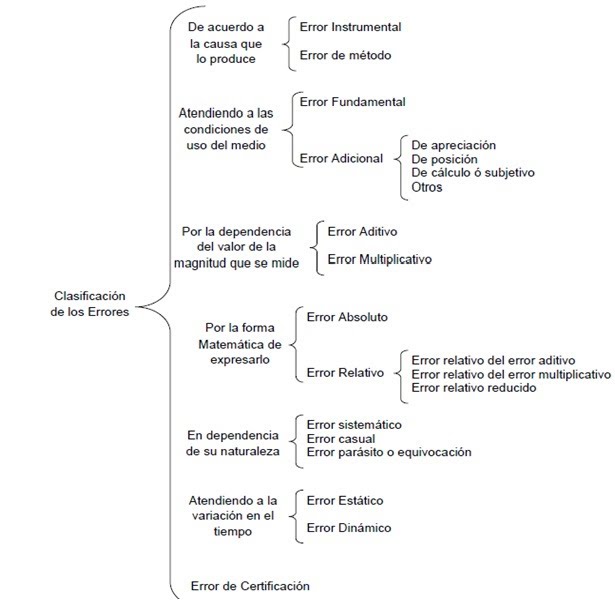
Errores en la medición
 |
¿Error? No … no lo midiste incorrecto … se trata de la precisión . |
¡Los instrumentos de medida no son exactos!
Grado de precisión
La precisión depende del instrumento con el que esté midiendo. Pero como regla general:
Ejemplos:
| Cuando su instrumento mide en “1” s entonces cualquier valor entre 6½ y 7½ se mide como “7” |
 |
| Cuando su instrumento mide en “2” s entonces cualquier valor entre 7 y 9 se mide como “8” |
 |
Observe que la flecha apunta al mismo punto, ¡pero los valores medidos son diferentes!
Más o menos
| Podemos mostrar el error usando el signo “Más o Menos”: | ± |
|
Cuando el valor podría estar entre 6½ y 7½ : 7 ± 0,5 El error es ± 0.5
|
 |
|
Cuando el valor podría estar entre 7 y 9 : 8 ± 1 El error es ± 1
|
 |

Ejemplo: una cerca se mide como 12.5 metros de largo, con una precisión de 0.1 de un metro
Preciso a 0.1 m significa que podría ser hasta 0.05 m de cualquier manera:
Longitud = 12.5 ± 0.05 m
Por lo tanto, podría tener entre 12,45 my 12,55 m de largo.
Error absoluto, relativo y de porcentaje
Pero … al medir no sabemos el valor real. Entonces usamos el máximo error posible.
En el ejemplo anterior, el error absoluto es 0,05 m
¿Qué pasó con el ± …? Bueno, solo queremos el tamaño (el valor absoluto ) de la diferencia.
No conocemos la medición real, por lo que lo mejor que podemos hacer es usar el valor medido :
Error relativo = [19459041 ] Error absoluto Valor medido
Veamos en un ejemplo:

Ejemplo: cerca (continuación)
Longitud = 12.5 ± 0.05 m
Entonces:
Error absoluto = 0,05 m
Y:
Error relativo = 0.05 m 12.5 m ] = 0,004
Y:
Error porcentual = 0,4%
Más ejemplos:

Ejemplo: el termómetro mide los 2 grados más cercanos. La temperatura se midió a 38 ° C
La temperatura puede ser de hasta 1 ° a cada lado de 38 ° (es decir, entre 37 ° y 39 °)
Temperatura = 38 ± 1 °
Entonces:
Error absoluto = 1 °
Y:
Error relativo = 1 ° 38 ° = 0,0263 …
Y:
Error de porcentaje = 2,63 …%
Ejemplo: Mides que la planta tenga 80 cm de altura (al cm más cercano)
Esto significa que podría estar equivocado hasta 0.5 cm (la planta podría tener entre 79.5 y 80.5 cm de alto)
Altura = 80 ± 0,5 cm
Entonces:
Error absoluto = 0,5 cm
Y:
Error relativo = 0,5 cm 80 cm = 0,00625
Y:
Porcentaje de error = 0.625%
Área
Cuando trabaje en áreas, debe tener en cuenta tanto el ancho como el largo … posiblemente podrían ser la medida más pequeña o ambas las más grandes.
Ejemplo: Alex midió el campo al metro más cercano y obtuvo un ancho de 6 my una longitud de 8 m.
Medir al medidor más cercano significa que el valor verdadero podría ser hasta medio metro más pequeño o más grande.
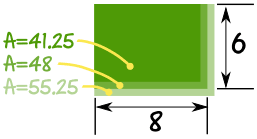
El ancho (w) podría ser de 5,5 ma 6,5 m:
La longitud (l) podría ser de 7,5 ma 8,5 m:
El área es ancho × largo:
El área más pequeña posible es: 5.5m × 7.5m = 41.25 m 2
El área medida es: 6m × 8m = 48 m 2
Y el área más grande posible es: 6.5m × 8.5m = 55.25 m 2
Error absoluto, relativo y de porcentaje
Lo único complicado aquí es … ¿cuál es el error absoluto?
- De 41.25 a 48 = 6.75
- De 48 a 55.25 = 7.25
Respuesta: ¡elige la más grande! Entonces:
Error absoluto = 7,25 m 2
Error relativo = 7,25 m 2 48 m 2 [19459051 ] = 0,151 …
Error porcentual = 15,1%
(¿Qué no es muy preciso, verdad?)
Volumen
Y el volumen tiene tres medidas: ancho, largo y alto .
Cada medida podría ser la medida más pequeña posible o la más grande.
Ejemplo: Sam midió la caja a los 2 cm más cercanos y obtuvo 24 cm × 24 cm × 20 cm
Medir a los 2 cm más cercanos significa que el valor verdadero podría ser hasta 1 cm más pequeño o más grande.
Las tres medidas son:
- 24 ± 1 cm
- 24 ± 1 cm
- 20 ± 1 cm
El volumen es ancho × largo × alto:
El volumen más pequeño posible es: 23cm × 23cm × 19cm = 10051 cm 3
El volumen medido es: 24 cm × 24 cm × 20 cm = 11520 cm 3
El mayor volumen posible es: 25cm × 25cm × 21cm = 13125 cm 3

Y así obtenemos:
Error absoluto, relativo y de porcentaje
Error absoluto:
- De 10051 a 11520 = 1469
- De 11520 a 13125 = 1605
Elige el más grande:
Error absoluto = 1605 cm 3
Error relativo = 1605 cm 3 11520 cm 3 [19459051 ] = 0,139 …
Error porcentual = 13,9%
