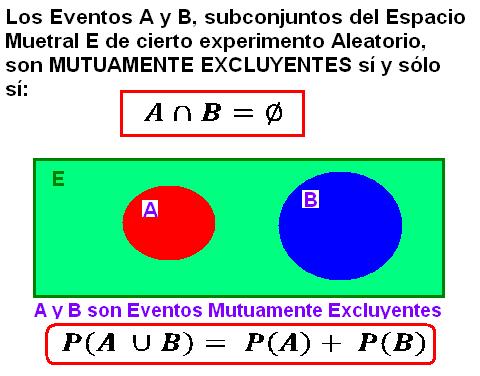
Eventos mutuamente exclusivos

Mutuamente excluyente : no puede suceder al mismo tiempo.
Ejemplos:
- Girar a la izquierda y girar a la derecha son mutuamente exclusivas (no se pueden hacer ambas cosas al mismo tiempo)
- Lanzar una moneda: cara y cruz son mutuamente excluyentes
- Cartas: Reyes y Ases son mutuamente exclusivos
¿Qué es no mutuamente excluyente:
- Girar a la izquierda y rascarse la cabeza puede ocurrir al mismo tiempo
- Reyes y Corazones, ¡porque podemos tener un Rey de Corazones!
Como aquí:
 |
 |
|
| Ases y reyes son Mutuamente excluyente (no pueden ser ambos) |
Corazones y reyes son no mutuamente excluyente (pueden ser ambos) |
Probabilidad
Veamos las probabilidades de eventos mutuamente excluyentes. Pero primero, una definición:
Probabilidad de que ocurra un evento =
Número de formas en que puede suceder
Número total de resultados
Ejemplo: hay 4 reyes en una baraja de 52 cartas. ¿Cuál es la probabilidad de elegir un rey?
Número de formas en que puede suceder: 4 (hay 4 Reyes)
Número total de resultados: 52 (hay 52 cartas en total)
Entonces la probabilidad =
4
52
=
1
13
Mutuamente exclusivo
Cuando dos eventos (llámalos “A” y “B”) son mutuamente excluyentes, es imposible que ocurran juntos:
P (A y B) = 0
“La probabilidad de A y B juntos es igual a 0 (imposible)”
Ejemplo: rey y reina
¡Una carta no puede ser un Rey Y una Reina al mismo tiempo!
- La probabilidad de un Rey y una Reina es 0 (Imposible)
Pero, para eventos mutuamente excluyentes, la probabilidad de A o B es la suma de las probabilidades individuales:
P (A o B) = P (A) + P (B)
“La probabilidad de A o B es igual a la probabilidad de A más la probabilidad de B”
Ejemplo: Rey O Reina
En una baraja de 52 cartas:
- la probabilidad de un Rey es 1/13, entonces P (Rey) = 1/13
- la probabilidad de una Reina también es 1/13, entonces P (Reina) = 1/13
Cuando combinamos esos dos eventos:
- La probabilidad de un Rey o una Reina es (1/13) + (1/13) = 2/13
Que se escribe así:
P (Rey o Reina) = (1/13) + (1/13) = 2/13
Entonces, tenemos:
- P (Rey y Reina) = 0
- P (Rey o Reina) = (1/13) + (1/13) = 2/13
Notación especial
En lugar de “y”, a menudo verá el símbolo ∩ (que es el símbolo de “intersección” utilizado en Diagramas de Venn )
En lugar de “o”, a menudo verá el símbolo ∪ (el símbolo de “Unión”)
Entonces también podemos escribir:
- P (Rey ∩ Reina) = 0
- P (Rey ∪ Reina) = (1/13) + (1/13) = 2/13

Ejemplo: objetivos de puntuación
Si la probabilidad de:
- sin goles (Evento “A”) es 20%
- anotando exactamente 1 gol (Evento “B”) es 15%
Entonces:
- La probabilidad de no marcar goles y 1 gol es 0 (Imposible)
- La probabilidad de no marcar goles o 1 gol es 20% + 15% = 35%
Que está escrito:
P (A ∩ B) = 0
P (A ∪ B) = 20% + 15% = 35%
Recordando
Para ayudarte a recordar, piensa:

“O tiene más … que Y ”
También ∪ es como una taza que contiene más que ∩
No mutuamente excluyente
Ahora veamos qué sucede cuando los eventos son no mutuamente excluyentes .
Ejemplo: corazones y reyes

|
Corazones y Los reyes juntos son solo el Rey de Corazones: |
 |
Pero Hearts o Kings es:
- todos los corazones (13 de ellos)
- todos los Reyes (4 de ellos)
¡Pero eso cuenta dos veces al Rey de Corazones!
Entonces corregimos nuestra respuesta, restando la parte “y” adicional:

16 Cartas = 13 Corazones + 4 Reyes – el 1 Rey de Corazones extra
¡Cuenta para asegurarte de que esto funcione!
Como fórmula, esto es:
P (A o B) = P (A) + P (B) – P (A y B)
“La probabilidad de A o B es igual
la probabilidad de A más la probabilidad de B
menos la probabilidad de A y B “
Aquí está la misma fórmula , pero usando ∪ y ∩ :
P (A ∪ B) = P (A) + P (B) – P (A ∩ B)
Un ejemplo final
16 personas estudian francés, 21 estudian español y hay 30 en total. ¡Resuelve las probabilidades!
Este es definitivamente un caso de no Mutuamente excluyentes (puedes estudiar francés y español).
Digamos que b es cuántos estudian ambos idiomas:
- las personas que estudian francés solo deben ser 16-b
- las personas que estudian español solamente deben ser 21-b
Y obtenemos:

Y sabemos que hay 30 personas, entonces:
Y podemos poner los números correctos:

Entonces sabemos todo esto ahora:
- P (francés) = 16/30
- P (español) = 21/30
- P (solo francés) = 30/9
- P (solo en español) = 14/30
- P (francés o español) = 30/30 = 1
- P (francés y español) = 30/7
Finalmente, verifiquemos con nuestra fórmula:
P (A o B) = P (A) + P (B) – P (A y B)
Ponga los valores en:
30/30 = 16/30 + 21/30 – 7/30
¡Sí, funciona!
Resumen:
Mutuamente exclusivo
- A y B juntos es imposible: P (A y B) = 0
- A o B es la suma de A y B: P (A o B) = P (A) + P (B)
No mutuamente excluyente
- A o B es la suma de A y B menos A y B: P (A o B) = P (A) + P (B) – P (A y B)
Símbolos
- Y es ∩ (el símbolo de “intersección”)
- O es ∪ (el símbolo de “Unión”)
