
Exponentes
El exponente de un número dice cuántas veces usar el número en una multiplicación.
En 8 2 el “2” dice que use 8 dos veces en una multiplicación,
entonces 8 2 = 8 × 8 = 64
En palabras: 8 2 podría llamarse “8 a la potencia 2” u “8 a la segunda potencia”, o
simplemente “8 al cuadrado”
Los exponentes también se denominan potencias o índices.
Algunos ejemplos más:
Ejemplo: 5 3 = 5 × 5 × 5 = 125
- En palabras: 5 3 podría llamarse “5 a la tercera potencia”, “5 a la potencia 3” o simplemente
“5 cubos”
Ejemplo: 2 4 = 2 × 2 × 2 × 2 = 16
- En palabras: 2 4 podría llamarse “2 a la cuarta potencia” o “2 a la potencia 4” o simplemente
“2 a la 4ta”
Los exponentes facilitan la escritura y el uso de muchas multiplicaciones
Ejemplo: 9 6 es más fácil de escribir y leer que 9 × 9 × 9 × 9 × 9 × 9
Puede multiplicar cualquier número por sí mismo tantas veces como desee utilizando exponentes.
Prueba aquí:
En general
Entonces en general :
| a n te dice que multipliques a por sí mismo, entonces hay n de esos a : |
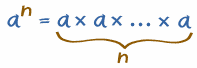 |
Otra forma de escribirlo
A veces las personas usan el símbolo ^ (arriba del 6 en su teclado), ya que es fácil de escribir.
Ejemplo: 2 ^ 4 es lo mismo que 2 4
- 2 ^ 4 = 2 × 2 × 2 × 2 = 16
Exponentes negativos
¿Negativo? ¿Qué podría ser lo contrario de multiplicar?
¡Dividiendo!
Un exponente negativo significa cuántas veces
divide uno entre el número.
Ejemplo: 8 -1 = 1 ÷ 8 = 0,125
Puedes tener muchas divisiones:
Ejemplo: 5 -3 = 1 ÷ 5 ÷ 5 ÷ 5 = 0,008
Pero eso se puede hacer de una manera más fácil:
5 -3 también podría calcularse como:
1 ÷ (5 × 5 × 5) = 1/5 3 = 1/125 = 0.008
¿Negativo? Voltear lo positivo!
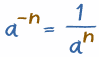 |
Ese último ejemplo mostró una manera más fácil de manejar exponentes negativos:
|
Más ejemplos:
| Exponente negativo | Recíproco de exponente positivo | Respuesta | ||
|---|---|---|---|---|
| 4 -2 | = | 1/4 2 | = | 1/16 = 0,0625 |
| 10 -3 | = | 1/10 3 | = | 1 / 1,000 = 0,001 |
| (-2) -3 | = | 1 / (-2) 3 | = | 1 / (- 8) = -0.125 |
¿Qué pasa si el exponente es 1 o 0?
| 1 | Si el exponente es 1, entonces solo tiene el número mismo (ejemplo 9 1 = 9 ) | |
| 0 | Si el exponente es 0, entonces obtienes 1 (ejemplo 9 0 = 1 ) | |
| Pero ¿qué pasa con 0 0 ? Podría ser 1 o 0, por lo que la gente dice que es “indeterminado” . |
Todo tiene sentido
Mi método favorito es comenzar con “1” y luego multiplicar o dividir tantas veces como dice el exponente, entonces obtendrá la respuesta correcta, por ejemplo:
| Ejemplo: potencias de 5 | |||
|---|---|---|---|
| .. etc. |  |
||
| 5 2 | 1 × 5 × 5 | 25 | |
| 5 1 | 1 × 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 ÷ 5 | 0,2 | |
| 5 -2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| .. etc. | |||
Si miras esa tabla, verás que los exponentes positivos, cero o negativos son realmente parte del mismo patrón (bastante simple).
Ten cuidado con la agrupación
Para evitar confusiones, use paréntesis () en casos como este:
| Con (): | (-2) 2 = (-2) × (-2) = 4 |
| Sin (): | -2 2 = – (2 2 ) = – (2 × 2) = -4 |
| Con (): | (ab) 2 = ab × ab |
| Sin (): | ab 2 = a × (b) 2 = a × b × b |

