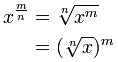Exponentes fraccionales
También llamado “Radicales” o “Exponentes racionales”
Exponentes de números enteros
Primero, veamos el número entero exponentes :

El exponente de un número dice cuántas veces usar el número en una multiplicación .
En este ejemplo: 8 2 = 8 × 8 = 64
simplemente “8 al cuadrado”
Otro ejemplo: 5 3 = 5 × 5 × 5 = 125
Exponentes fraccionales
¿Pero qué pasa si el exponente es una fracción?
|
Un exponente de 1 2 es en realidad raíz cuadrada Un exponente de 1 3 es raíz cúbica Un exponente de 1 4 es 4ta raíz ¡Y así sucesivamente! |
 |
¿Por qué?
Veamos por qué en un ejemplo.
Primero, las Leyes de exponentes nos dicen cómo manejar exponentes cuando multiplicamos:
Ejemplo: x 2 x 2 = (xx) (xx) = xxxx = x 4
Lo que muestra que x 2 x 2 = x (2 + 2) = x 4
Entonces intentemos eso con exponentes fraccionales:
Ejemplo: ¿Cuál es 9 ½ × 9 ½ ?
9 ½ × 9 ½ = 9 (½ + ½) = 9 (1) = 9 [ 19459024]
Entonces 9 ½ veces da 9
¿Cómo llamamos a un número que, cuando se multiplica por sí mismo, da otro número? ¡La raíz cuadrada !
Ver:
√9 × √9 = 9
Y:
9 ½ × 9 ½ = 9
Entonces 9 ½ es lo mismo que √9
Pruebe con otra fracción
Intentemos eso de nuevo, pero con un exponente de un cuarto (1/4):
Ejemplo:
16 ¼ × 16 ¼ × 16 ¼ × 16 ¼ = 16 (¼ + ¼ + ¼ + ¼) = 16 (1) = 16
Entonces 16 ¼ usado 4 veces en una multiplicación da 16,
y así 16 ¼ es una cuarta raíz de 16
Regla general
Funcionó para ½ , trabajó con ¼ , de hecho funciona en general:
x 1 / n = La n- th Raíz de x
Entonces podemos llegar a esto:
| |
|
Ejemplo: ¿Qué es 27 1/3 ?
Respuesta: 27 1/3 = 27 = 3
¿Qué pasa con las fracciones más complicadas?
¿Qué pasa con un exponente fraccional como 4 3/2 ?
Eso realmente dice hacer un cubo (3) y una raíz cuadrada (1/2), en cualquier orden.
Déjame explicarte.
Una fracción (como m / n ) se puede dividir en dos partes:
- una parte de número entero ( m ) y
- una fracción ( 1 / n ) parte
Entonces, porque m / n = m × (1 / n) podemos hacer esto:
El orden no importa, por lo que también funciona para m / n = (1 / n) × m :
Y obtenemos esto:
| |
|
Algunos ejemplos:
Ejemplo: ¿Qué es 4 3/2 ?
4 3/2 = 4 3 × (1/2) = √ (4 3 ) = √ (4 × 4 × 4) = √ (64) = 8
o
4 3/2 = 4 (1/2) × 3 = (√4) 3 = (2) 3 [19459017 ] = 8
De cualquier manera se obtiene el mismo resultado.
Ejemplo: ¿Qué es 27 4/3 ?
27 4/3 = 27 4 × (1/3) = (27 4 ) =
( 531441) = 81
o
27 4/3 = 27 (1/3) × 4 = ( 27) 4 = (3) 4 = 81
¡Ciertamente fue más fácil la segunda manera!
Ahora … ¡juega con el gráfico!
Mira cómo suavemente la curva cambia cuando juegas con las fracciones en esta animación, esto te muestra que esta idea de exponentes fraccionales encaja perfectamente:
Cosas para probar:
- Comienza con m = 1 yn = 1, luego aumenta lentamente n para que puedas ver 1/2, 1/3 y 1/4
- Luego prueba m = 2 y desliza n hacia arriba y hacia abajo para ver fracciones como 2/3, etc.
- Ahora intenta hacer el exponente -1
- Finalmente intente aumentar m, luego reduzca n, luego reduzca m, luego aumente n: la curva debe dar vueltas y vueltas