
Expresiones racionales
Una expresión que es la relación de dos polinomios :

Es como una fracción, pero con polinomios.
Otros ejemplos:
| x 3 + 2x – 1 6x 2 | 2x + 9 x 4 – x 2 |
También
| 1 2 – x 2 | El polinomio superior es “1”, que está bien. |
| 2x 2 + 3 | ¡Sí lo es! Como también podría escribirse: 2x 2 + 3 1 |
Pero no
| |
2 – √ (x) 4 – x | la parte superior no es un polinomio (no se permite la raíz cuadrada de una variable) |
| |
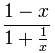 |
1 / x no está permitido en un polinomio |
En general
Una función racional es la relación de dos polinomios P (x) y Q (x) como este
f (x) = P (x) Q (x)
Excepto que Q (x) no puede ser cero (y en cualquier lugar que Q (x) = 0 no está definido)
Encontrar raíces de expresiones racionales
|
Una “raíz” (o “cero”) es donde la expresión es igual a cero : |
 |
Para encontrar las raíces de una Expresión racional solo necesitamos encontrar las raíces del polinomio superior , siempre que la Expresión racional esté en “Términos más bajos”.
Entonces, ¿qué significa “Términos más bajos”?
Términos más bajos
Bueno, una fracción está en los términos más bajos cuando la parte superior e inferior no tienen factores comunes.
Ejemplo: fracciones
2
6
es no en los términos más bajos,
como 2 y 6 tienen el factor común “2”
Pero:
1
3
es en los términos más bajos,
como 1 y 3 no tienen factores comunes
Asimismo, una Expresión racional está en los términos más bajos cuando la parte superior e inferior no tienen factores comunes.
Ejemplo: expresiones racionales
x 3 + 3x 2 2x es no en los términos más bajos ,
como x 3 + 3x 2 y 2x
tienen el factor común “x”
Pero
x 2 + 3x 2 es en los términos más bajos,
como x 2 + 3x y 2 no tienen factores comunes
Entonces, para encontrar las raíces de una expresión racional :
- Reduzca la expresión racional a los términos más bajos,
- Luego encuentra las raíces del polinomio superior
¿Cómo encontramos raíces? Lea Resolviendo polinomios para aprender cómo.
Propia vs impropia
| Las fracciones pueden ser apropiadas o impropias : |
 |
| (No hay nada malo con “Incorrecto”, es solo un tipo diferente) |
Y asimismo:
Una expresión racional también puede ser propiamente dicha o impropia .
Pero, ¿qué hace que un polinomio sea más grande o más pequeño?
¡El Grado !
Para un polinomio con una variable, el grado es el mayor exponente de esa variable.
Ejemplos de grado:
| 4x | El grado es 1 (una variable sin exponente en realidad tiene un exponente de 1) |
|
| 4x 3 – x + 3 | El grado es 3 (máximo exponente de x) |
Entonces, esto es cómo saber si una expresión racional es apropiada o impropia :
Apropiado : el grado de la parte superior es menor que el grado de la parte inferior.
| Apropiado: | 1 x + 1 | grados (arriba) < grados (abajo) |
Otro ejemplo: x x 3 – 1
Incorrecto : el grado de la parte superior es mayor o igual que el grado de la parte inferior.
| Incorrecto: | x 2 – 1 x + 1 | grados (arriba) ≥ grados (abajo) |
Otro ejemplo: 4x 3 – 3 5x 3 + 1
Si el polinomio es incorrecto, podemos simplificarlo con División larga polinómica
Asíntotas
Las expresiones racionales pueden tener asíntotas (una línea que se aproxima a una curva mientras se dirige hacia el infinito) :
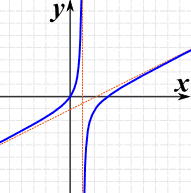
Ejemplo: (x 2 -3x) / (2x-2)
|
El gráfico de (x 2 -3x) / (2x-2) tiene:
|
 |
Una expresión racional puede tener:
- cualquier número de asíntotas verticales,
- solo cero o una asíntota horizontal,
- solo cero o una asíntota oblicua (inclinada)
Encontrar asíntotas horizontales u oblicuas
Es bastante fácil encontrarlos …
… pero depende de el grado del polinomio superior vs inferior .
El que tenga el mayor grado crecerá más rápido.
Al igual que “Proper” e “Improper”, pero de hecho hay cuatro casos posibles, que se muestran a continuación.
(Muestro un valor de prueba de x = 1000 para cada caso, solo para mostrar lo que sucede)
Veamos cada uno de esos ejemplos a su vez:
Grado superior Menos que inferior
El polinomio inferior dominará, y hay una asíntota horizontal en cero.
Ejemplo: f (x) = (3x + 1) / (4x 2 +1)
Cuando x es 1000:
f (1000) = 3001/4000001 = 0,00075 …
Y a medida que x aumenta, f (x) se acerca a 0
El grado de parte superior es igual a parte inferior
Ninguno de los dos domina … la asíntota se establece mediante los términos principales de cada polinomio.
Ejemplo: f (x) = (3x + 1) / (4x + 1)
Cuando x es 1000:
f (1000) = 3001/4001 = 0,750 …
Y a medida que x se hace más grande, f (x) se acerca a 3/4
¿Por qué 3/4? Porque “3” y “4” son los “coeficientes principales” de cada polinomio
Los términos están en orden de mayor a menor exponente
(Técnicamente, el 7 es una constante, pero aquí es más fácil pensar en todos ellos como coeficientes).
El método es fácil:
Divida el coeficiente principal del polinomio superior por el coeficiente principal del polinomio inferior.
Aquí hay otro ejemplo:
Ejemplo: f (x) = (8x 3 + 2x 2 – 5x + 1) / (2x 3 + 15x + 2) [19459043 ]
Los grados son iguales (ambos tienen un grado de 3)
Solo mira los coeficientes principales de cada polinomio:
- La parte superior es 8 (de 8x 3 )
- La parte inferior es 2 (de 2x 3 )
Entonces hay una asíntota horizontal en 8/2 = 4
El grado superior es 1 mayor que inferior
Este es un caso especial: hay una asíntota oblicua , y necesitamos encontrar la ecuación de la línea.
Para resolverlo, usa división larga polinómica : divide la parte superior por la parte inferior para encontrar el cociente (ignora el resto).
Ejemplo: f (x) = (3x 2 +1) / (4x + 1)
El grado de la parte superior es 2, y el grado de la parte inferior es 1, por lo que no habrá una asíntota oblicua
Necesitamos dividir 3x 2 +1 por 4x + 1 usando la división larga polinómica:
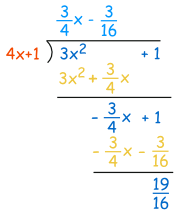
La respuesta es (3/4) x- (3/16) (ignorando el resto):
La ”ecuación de línea” de la asíntota es: (3/4) x- (3/16)
El grado superior es Más de 1 mayor que inferior
Cuando el polinomio superior es más de 1 grado más alto que el polinomio inferior, no hay ninguna asíntota horizontal u oblicua .
Ejemplo: f (x) = (3x 3 +1) / (4x + 1)
El grado de la parte superior es 3, y el grado de la parte inferior es 1.
La parte superior es más de 1 grado más alta que la parte inferior, por lo que no hay ninguna asíntota horizontal u oblicua .
Encontrar asíntotas verticales
Hay otro tipo de asíntota, que es causada por el polinomio inferior solamente .
Pero primero: ¡asegúrese de que la expresión racional esté en los términos más bajos!

Cuando el polinomio inferior es igual a cero (cualquiera de sus raíces) obtenemos una asíntota vertical.
Lea Resolviendo polinomios para aprender cómo encontrar las raíces
De nuestro ejemplo anterior:
Ejemplo: (x 2 -3x) / (2x-2)
|
El polinomio inferior es 2x-2 , que se factoriza en: 2 (x-1) Y el factor (x-1) significa que hay una asíntota vertical en x = 1 (porque 1-1 = 0) |
 |
Un ejemplo completo
Ejemplo: Croquis (x − 1) / (x 2 −9)
En primer lugar, podemos factorizar el polinomio inferior (es la diferencia de dos cuadrados):
x − 1 (x + 3) (x − 3)
Ahora podemos ver:
Las raíces del polinomio superior son: +1 (aquí es donde cruza el eje x )
Las raíces del polinomio inferior son: −3 y +3 (estas son asíntotas verticales )
cruza el eje y cuando x = 0, así que establezcamos x en 0:
Cruza el eje y en:
0−1 (0 + 3) (0−3) = −1 −9 ] = 1 9
También sabemos que el grado de la parte superior es menor que el grado de la parte inferior, por lo que hay una asíntota horizontal en 0
Para que podamos esbozar toda esa información:

Y ahora podemos dibujar en la curva:

(Compare eso con la gráfica de (x-1) / (x 2 -9) )


