
Factoring en álgebra
Factores
Los números tienen factores :

Y las expresiones (como x 2 + 4x + 3 ) también tienen factores:

Factoring
Factoring (llamado “ Factoring ” en el Reino Unido) es el proceso de encontrar los factores :
Factoring: encontrar qué multiplicar para obtener una expresión.
Es como “dividir” una expresión en una multiplicación de expresiones más simples.
Ejemplo: factor 2y + 6
Tanto 2y como 6 tienen un factor común de 2:
- 2y es 2 × y
- 6 es 2 × 3
Entonces podemos factorizar toda la expresión en:
2y + 6 = 2 (y + 3)
Entonces 2y + 6 ha sido “factorizado en” 2 y y + 3
Factoring es también lo opuesto a Expandiendo :

Factor común
En el ejemplo anterior vimos que 2y y 6 tenían un factor común de 2
Pero para hacer el trabajo correctamente necesitamos el factor común más alto , incluidas las variables
Ejemplo: factor 3y 2 + 12y
En primer lugar, 3 y 12 tienen un factor común de 3 .
Entonces podríamos tener:
3y 2 + 12y = 3 (y 2 + 4y)
¡Pero podemos hacerlo mejor!
3y 2 y 12y también comparten la variable y .
Juntos, eso hace que 3 años :
- 3y 2 es 3y × y
- 12y es 3y × 4
Entonces podemos factorizar toda la expresión en:
3y 2 + 12y = 3y (y + 4)
Verificar: 3y (y + 4) = 3y × y + 3y × 4 = 3y 2 + 12y
Factoring más complicado
Factoring puede ser difícil!
Los ejemplos han sido simples hasta ahora, pero factorizar puede ser muy complicado.
¡Porque tenemos que calcular lo que se multiplicó para producir la expresión que se nos da!
Es como tratar de encontrar qué ingredientes
entró en un pastel para hacerlo tan delicioso.
¡Puede ser difícil de entender!
La experiencia ayuda
Con más experiencia, la factorización se vuelve más fácil.
Ejemplo: Factor 4x 2 – 9
Hmmm … no parece haber ningún factor común.
Pero conocer los Productos binomiales especiales nos da una pista llamada “diferencia de cuadrados” :
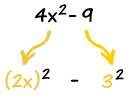
Porque 4x 2 es (2x) 2 , y 9 es (3 ) 2 ,
Entonces tenemos:
4x 2 – 9 = (2x) 2 – (3) 2
Y eso puede ser producido por la fórmula de la diferencia de cuadrados:
(a + b) (a − b) = a 2 – b 2
Donde a es 2x, y b es 3.
Así que intentemos hacer eso:
(2x + 3) (2x − 3) = (2x) 2 – (3) 2 = 4x 2 – 9
¡Sí!
Entonces, los factores de 4x 2 – 9 son (2x + 3) y (2x − 3) : [19459008 ]
Respuesta: 4x 2 – 9 = (2x + 3) (2x − 3)
¿Cómo puedes aprender a hacer eso? ¡Obteniendo mucha práctica y conociendo “Identidades”!
Recuerde estas identidades
Aquí hay una lista de “Identidades” comunes (incluida la “diferencia de cuadrados” utilizada anteriormente).
Vale la pena recordarlos, ya que pueden facilitar la factorización.
 |
||
| a 2 – b 2 | = | (a + b) (a − b) |
| a 2 + 2ab + b 2 | = | (a + b) (a + b) |
| a 2 – 2ab + b 2 | = | (a − b) (a − b) |
| a 3 + b 3 | = | (a + b) (a 2 −ab + b 2 ) |
| a 3 – b 3 | = | (a − b) (a 2 + ab + b 2 ) |
| a 3 + 3a 2 b + 3ab 2 + b 3 | = | (a + b) 3 |
| a 3 −3a 2 b + 3ab 2 −b 3 | = | (a − b) 3 |
Hay muchos más como esos, pero esos son los más útiles.
Consejo
La forma factorizada suele ser la mejor.
Cuando intentes factorizar, sigue estos pasos:
- “Factorizar” cualquier término común
- Vea si se ajusta a alguna de las identidades, más cualquier otra información que pueda conocer
- Continúa hasta que no puedas factorizar más
También hay sistemas de álgebra computacional (llamados “CAS”) como Axiom, Derive, Macsyma, Maple, Mathematica, MuPAD, Reduce y muchos más que son buenos para factorizar.
Más ejemplos
La experiencia ayuda, así que aquí hay más ejemplos para ayudarte en el camino:
Ejemplo: w 4 – 16
¿Un exponente de 4? Tal vez podríamos probar un exponente de 2:
w 4 – 16 = (w 2 ) 2 – 4 2
Sí, es la diferencia de cuadrados
w 4 – 16 = (w 2 + 4) (w 2 – 4)
Y “(w 2 – 4)” es otra diferencia de cuadrados
w 4 – 16 = (w 2 + 4) (w + 2) (w [19459013 ] – 2)
Eso es todo lo que puedo llegar (a menos que use números imaginarios)
Ejemplo: 3u 4 – 24uv 3
Eliminar factor común “3u”:
3u 4 – 24uv 3 = 3u (u 3 – 8v 3 )
Entonces una diferencia de cubos:
3u 4 – 24uv 3 = 3u (u 3 – (2v) 3 )
= 3u (u − 2v) (u 2 + 2uv + 4v 2 )
Eso es lo más lejos que puedo llegar.
Ejemplo: z 3 – z 2 – 9z + 9
Intenta factorizar los dos primeros y los dos segundos por separado:
z 2 (z − 1) – 9 (z − 1)
Wow, (z-1) está en ambos, así que usemos eso:
(z 2 −9) (z − 1)
Y z 2 −9 es una diferencia de cuadrados
(z − 3) (z + 3) (z − 1)
Eso es lo más lejos que puedo llegar.
Ahora obtén más experiencia:
