
Intervalos de confianza

Un intervalo de 4 más o menos 2
Un intervalo de confianza es un rango de valores estamos bastante seguros de que nuestro valor verdadero se encuentra.

Ejemplo: altura media
Medimos las alturas de 40 hombres elegidos al azar, y obtenemos una media altura de 175cm ,
También sabemos que la desviación estándar de las alturas de los hombres es 20 cm .
El intervalo de confianza del 95% (mostramos cómo calcularlo más adelante) es:
175 cm ± 6,2 cm
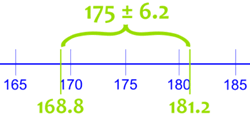
Esto dice que la verdadera media de TODOS los hombres (si pudiéramos medir todas sus alturas) es probable que esté entre 168.8cm y 181.2cm.
¡Pero puede que no sea así!
El “95%” dice que el 95% de los experimentos como acabamos de hacer incluirá la media real, pero el 5% no .
Por lo tanto, existe una probabilidad de 1 en 20 (5%) de que nuestro intervalo de confianza NO incluya la media real.
Cálculo del intervalo de confianza
Paso 1 : comienza con
- el número de observaciones n
- la media X
- y la desviación estándar s
Nota: deberíamos usar la desviación estándar de toda la población , pero en muchos casos no lo sabremos.
Podemos usar la desviación estándar para la muestra si tenemos suficientes observaciones (al menos n = 30, con suerte más).
Usando nuestro ejemplo:
- número de observaciones n = 40
- media X = 175
- desviación estándar s = 20
Paso 2 : decida qué intervalo de confianza queremos: 95% o 99% son opciones comunes. Luego encuentre el valor “Z” para ese intervalo de confianza aquí:
| Confianza Intervalo |
Z |
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99,5% | 2.807 |
| 99,9% | 3.291 |
Para el 95%, el valor Z es 1.960
Paso 3 : use ese valor Z en esta fórmula para el intervalo de confianza
X ± Z s √n
Dónde:
- X es la media
- Z es el valor Z elegido de la tabla anterior
- s es la desviación estándar
- n es el número de observaciones
Y tenemos:
175 ± 1.960 × 20 √40
Que es:
175 cm ± 6,20 cm
En otras palabras: de 168,8 cm a 181,2 cm
El valor después de ± se llama margen de error
El margen de error en nuestro ejemplo es 6.20cm

Calculadora
Tenemos una Calculadora de intervalo de confianza para hacerte la vida más fácil.
Simulador
También tenemos un simulador de distribución normal muy interesante . donde podemos comenzar con una media “verdadera” teórica y una desviación estándar, y luego tomar muestras aleatorias.
Nos ayuda a comprender cómo las muestras aleatorias a veces pueden ser muy buenas o malas para representar los valores verdaderos subyacentes.
Otro ejemplo

Ejemplo: huerto de manzanas
¿Son las manzanas lo suficientemente grandes?
Hay cientos de manzanas en los árboles, por lo que elige al azar solo 46 manzanas y obtiene:
- una media de 86
- una desviación estándar de 6.2
Entonces, calculemos:
X ± Z s √n
Sabemos:
- X es la media = 86
- Z es el valor Z = 1,960 (de la tabla anterior para el 95%)
- s es la desviación estándar = 6,2
- n es el número de observaciones = 46
86 ± 1.960 × 6.2 √46 = 86 ± 1.79
Entonces, la verdadera media (de todos los cientos de manzanas) es probablemente entre 84,21 y 87,79
Media verdadera
Ahora imagina que podemos recoger TODAS las manzanas de inmediato y hacer que TODAS sean medidas por la empaquetadora (¡esto es un lujo que normalmente no se encuentra en las estadísticas!)
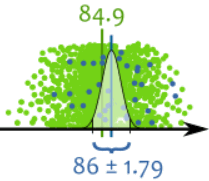
Y la verdadera media resulta ser 84,9
Pongamos todas las manzanas en el suelo desde la más pequeña a la más grande:
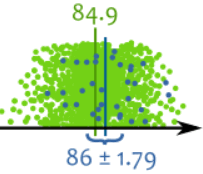
Cada manzana es un punto verde,
excepto nuestras observaciones que son azules
Nuestro resultado no fue exacto … es aleatorio después de todo … pero la verdadera media está dentro de nuestro intervalo de confianza de 86 ± 1.79 (en otras palabras, 84.21 a 87.79)
Pero la verdadera media podría no ser dentro del intervalo de confianza, pero ¡95% del tiempo lo hará!
El 95% de todos los “intervalos de confianza del 95%” incluirán la media real.
Tal vez tuvimos esta muestra, con una media de 83.5:
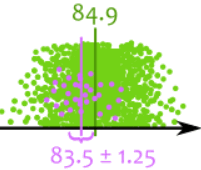
Cada manzana es un punto verde,
nuestras observaciones están marcadas en morado
Que no incluye la verdadera media. Espere que eso suceda el 5% del tiempo para un intervalo de confianza del 95%.
Entonces, ¿cómo sabemos si la muestra que tomamos es una del 95% “afortunada” o del 5% desafortunada? A menos que podamos medir a toda la población como arriba, simplemente no lo sabemos .
Este es el riesgo en el muestreo , podríamos tener una mala muestra.
Ejemplo en investigación
Aquí está el intervalo de confianza utilizado en investigaciones reales sobre ejercicio adicional para personas mayores :

¿Qué está diciendo? Mirando la línea “Macho” vemos:
- 1,226 Hombres (47.6% de todas las personas)
- tenía un “HR” (ver más abajo) con una media de 0,92 ,
- y un intervalo de confianza del 95% (IC 95%) de 0,88 a 0,97 (que también es 0,92 ± 0,05)
“HR” es una medida del beneficio para la salud (menor es mejor), por lo que esa línea dice que el verdadero beneficio del ejercicio (para la población más amplia de hombres) tiene un 95% de posibilidades de estar entre 0,88 y 0,97
* Nota para los curiosos: “HR” se usa mucho en la investigación de la salud y significa “Hazard Ratio” donde más bajo es mejor, por lo que un HR de 0.92 significa que los sujetos estaban mejor y 1.03 significa un poco peor apagado.
Distribución normal estándar
Todo se basa en la idea de la Distribución Normal Estándar , donde el valor Z es el “puntaje Z”
Por ejemplo, el Z para el 95% es 1.960, y aquí vemos que el rango de -1.96 a +1.96 incluye el 95% de todos los valores:
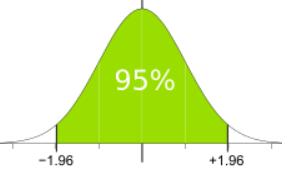
De -1.96 a +1.96 desviaciones estándar es 95%
Aplicar eso a nuestra muestra se ve así:
También de -1.96 a +1.96 desviaciones estándar, por lo que incluye 95%
Conclusión
El intervalo de confianza se basa en la media y la desviación estándar. Su fórmula es:
X ± Z s √n
Dónde:
- X es la media
- Z es el valor Z de la tabla a continuación
- s es la desviación estándar
- n es el número de observaciones
| Confianza Intervalo |
Z |
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99,5% | 2.807 |
| 99,9% | 3.291 |
