
Introducción a la trigonometría
Trigonometría (del griego trigonon “triángulo” + metron “medida”)
¿Quieres aprender trigonometría? Aquí hay un resumen rápido.
Siga los enlaces para obtener más información o vaya al Índice de trigonometría
 |
Trigonometría … se trata de triángulos . |
La trigonometría nos ayuda a encontrar ángulos y distancias, ¡y se usa mucho en ciencia, ingeniería, videojuegos y más!
Triángulo en ángulo recto
El triángulo de mayor interés es el triángulo rectángulo . El pequeño ángulo en la esquina muestra el ángulo recto:

Otro ángulo a menudo se etiqueta θ , y los tres lados se llaman entonces:
- Adyacente : adyacente (al lado) del ángulo θ
- Opuesto : opuesto al ángulo θ
- y el lado más largo es la Hipotenusa
¿Por qué un triángulo rectángulo?
¿Por qué es tan importante este triángulo?
Imagina que podemos medir a lo largo y hacia arriba pero queremos saber la distancia directa y el ángulo:

La trigonometría puede encontrar ese ángulo y distancia faltantes.
O tal vez tenemos una distancia y un ángulo y necesitamos “trazar el punto” a lo largo y hacia arriba:

Preguntas como estas son comunes en ingeniería, animación por computadora y más.
¡Y la trigonometría da las respuestas!
Seno, coseno y tangente
Las funciones principales en trigonometría son Seno, coseno y tangente
Son simplemente un lado de un triángulo rectángulo dividido por otro.
Para cualquier ángulo “ θ “:

(Seno, coseno y tangente a menudo se abrevian como sin, cos y tan .)
Ejemplo: ¿Cuál es el seno de 35 °?
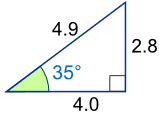
Usando este triángulo (las longitudes son solo un decimal):
sin (35 °) = Opuesto Hipotenusa = 2.8 4.9 = 0,57 …
El triángulo podría ser más grande, más pequeño o volteado, pero ese ángulo siempre tendrá esa relación .
Las calculadoras tienen sen, cos y tan para ayudarnos, así que veamos cómo usarlas:

Ejemplo: ¿Qué altura tiene el árbol?
No podemos llegar a la cima del árbol, así que nos alejamos y medimos un ángulo (usando un transportador) y una distancia (usando un láser):
- Conocemos la Hipotenusa
- Y queremos saber el Opuesto
Seno es la relación de Opuesto / Hipotenusa :
sin (45 °) =
Opuesto
Hipotenusa

Obtenga una calculadora, escriba “45”, luego la tecla “sin”:
sin (45 °) = 0,7071 …
¿Qué significa 0.7071 … ? Es la relación de las longitudes de los lados, por lo que el Opuesto es aproximadamente 0.7071 veces más largo que la Hipotenusa.
Ahora podemos poner 0.7071 … en lugar de pecado (45 °):
0.7071 … = Opuesto Hipotenusa
Y también sabemos que la hipotenusa es 20 :
0.7071 … = Opuesto 20
Para resolver, primero multiplique ambos lados por 20:
20 × 0,7071 … = Opuesto
Finalmente:
Opuesto = 14.14m (a 2 decimales)
Cuando ganes más experiencia, puedes hacerlo rápidamente así:

Ejemplo: ¿Qué altura tiene el árbol?
Opuesto
Hipotenusa
Opuesto
20
Opuesto
20
= 0,7071 …
El árbol tiene 14,14 m de altura
Prueba Sin Cos y Tan
Juega con esto por un tiempo (mueve el mouse) y familiarízate con los valores de seno, coseno y tangente para diferentes ángulos, como 0 °, 30 °, 45 °, 60 ° y 90 °.
Pruebe también 120 °, 135 °, 180 °, 240 °, 270 °, etc., y observe que las posiciones pueden ser positivas o negativas según las reglas de Coordenadas cartesianas , entonces el seno, el coseno y la tangente cambian entre positivo y negativo también.
¡Entonces trigonometría también se trata de círculos !

Círculo de unidades
Lo que acabas de jugar es el Unit Circle .
Es un círculo con un radio de 1 con su centro en 0.
Debido a que el radio es 1, podemos medir directamente seno, coseno y tangente.
Aquí vemos la función seno realizada por el círculo unitario:
Nota: puede ver los bonitos gráficos hechos por seno, coseno y tangente .
Grados y radianes
Los ángulos pueden estar en grados o radianes . Estos son algunos ejemplos:
| Ángulo | Grados | Radianes |
|---|---|---|
| |
90 ° | π / 2 |
| __ Ángulo recto | 180 ° | π |
| |
360 ° | 2 π |
Patrón repetitivo
Debido a que el ángulo gira alrededor del círculo , las funciones seno, coseno y tangente se repiten una vez cada rotación completa (ver Amplitud, período, cambio de fase y frecuencia ).

Cuando queremos calcular la función para un ángulo mayor que una rotación completa de 360 ° (2 π radianes), restamos tantas rotaciones completas como sea necesario para que vuelva a estar por debajo de 360 ° (2 [ 19459077] π radianes):
Ejemplo: ¿cuál es el coseno de 370 °?
370 ° es mayor que 360 °, así que restemos 360 °
370 ° – 360 ° = 10 °
cos (370 °) = cos (10 °) = 0.985 (a 3 decimales)
Y cuando el ángulo es menor que cero, simplemente agregue rotaciones completas.
Ejemplo: ¿cuál es el seno de −3 radianes?
−3 es menor que 0 así que agreguemos 2 π radianes
−3 + 2 π = −3 + 6.283 … = 3.283 … rad ians
sin (−3) = sin (3.283 …) = −0.141 (con 3 decimales)
Resolviendo triángulos
La trigonometría también es útil para triángulos generales, no solo en ángulo recto.
Nos ayuda en Resolviendo triángulos . “Resolver” significa encontrar lados y ángulos faltantes.
Ejemplo: encontrar el ángulo faltante “C”
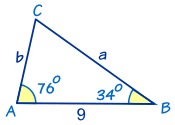
El ángulo C se puede encontrar usando los ángulos de un triángulo suman 180 ° :
Entonces C = 180 ° – 76 ° – 34 ° = 70 °
También podemos encontrar longitudes laterales faltantes. La regla general es:
Cuando conocemos 3 de los lados o ángulos, podemos encontrar los otros 3
(excepto el caso de los tres ángulos)
Ver Solucionar triángulos para más detalles.
Otras funciones (cotangente, secante, cosecante)
Similar a Seno, Coseno y Tangente, hay otras tres funciones trigonométricas que se hacen dividiendo un lado por otro:

|
Función Cosecante:
|
csc ( θ ) = Hipotenusa / Opuesto |
|
Función Secante:
|
seg ( θ ) = Hipotenusa / Adyacente |
|
Función cotangente:
|
cuna ( θ ) = Adyacente / Opuesto |
Identidades trigonométricas y triangulares
Y a medida que mejoras en la trigonometría puedes aprender esto:
 |
Las Identidades trigonométricas son ecuaciones que son verdaderas para todos los triángulos rectángulos . |
 |
Las Identidades de triángulos son ecuaciones que son verdaderas para todos los triángulos (no tienen que tener un ángulo recto). |
¡Disfruta convirtiéndote en un experto en triángulos (y círculos)!
