Leyes de exponentes
Los exponentes también se denominan Poderes o Índices

El exponente de un número dice cuántas veces usar el número en una multiplicación .
En este ejemplo: 8 2 = 8 × 8 = 64
simplemente “8 al cuadrado”
Pruébelo usted mismo:
¡Así que un exponente nos ahorra al escribir muchas multiplicaciones!
Ejemplo: a 7
a 7 = a × a × a × a × a × a × a = aaaaaaa
¿Observa cómo escribimos las letras juntas para significar multiplicar? Haremos mucho eso aquí.
Ejemplo: x 6 = xxxxxx
La clave de las leyes
Escribir todas las letras es la clave para entender las Leyes
Ejemplo: x 2 x 3 = (xx) (xxx) = xxxxx = x 5
Lo que muestra que x 2 x 3 = x 5 , ¡pero más sobre eso más adelante!
Entonces, en caso de duda, solo recuerda escribir todas las letras (todas las que te indique el exponente) y ver si puedes entenderlo.
Todo lo que necesitas saber …
Las “Leyes de los exponentes” (también llamadas “Reglas de los exponentes”) provienen de tres ideas :
| |
El exponente dice cuántas veces usar el número en una multiplicación . | ||
| |
Un exponente negativo significa dividir , porque lo contrario de multiplicar es dividir | ||
| |
|
Si entiendes eso, entonces entiendes exponentes!
Y todas las leyes a continuación se basan en esas ideas.
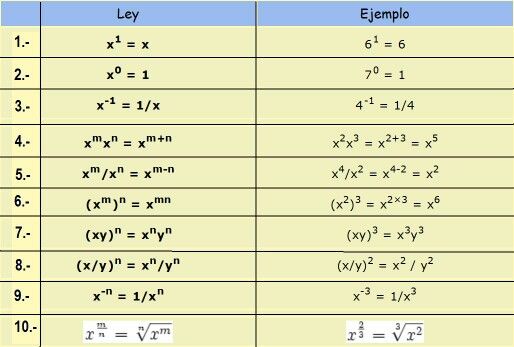
Leyes de exponentes
Aquí están las leyes
(Siguen las explicaciones):
| Ley | Ejemplo |
|---|---|
| x 1 = x | 6 1 = 6 |
| x 0 = 1 | 7 0 = 1 |
| x -1 = 1 / x | 4 -1 = 1/4 |
| x m x n = x m + n | x 2 x 3 = x 2 + 3 = x 5 |
| x m / x n = x m-n | x 6 / x 2 = x 6-2 = x 4 |
| (x m ) n = x mn | (x 2 ) 3 = x 2 × 3 = x 6 |
| (xy) n = x n y n | (xy) 3 = x 3 y 3 |
| (x / y) n = x n / y n | (x / a) 2 = x 2 / a 2 |
| x -n = 1 / x n | x -3 = 1 / x 3 |
| Y la ley sobre exponentes fraccionales: | |
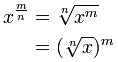 |
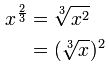 |
Leyes explicadas
Las tres primeras leyes anteriores ( x 1 = x , x 0 = 1 y x -1 = 1 / x ) son solo parte de la secuencia natural de exponentes. Echa un vistazo a esto:
| Ejemplo: potencias de 5 | |||
|---|---|---|---|
| .. etc. |  |
||
| 5 2 | 1 × 5 × 5 | 25 | |
| 5 1 | 1 × 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 ÷ 5 | 0.2 | |
| 5 -2 | 1 ÷ 5 ÷ 5 | 0,04 | |
| .. etc. | |||
Mire esa tabla por un tiempo … observe que los exponentes positivos, cero o negativos son realmente parte del mismo patrón, es decir, 5 veces más grande (o 5 veces más pequeño) dependiendo de si el exponente se hace más grande (o más pequeño) .
La ley que x m x n = x m + n
Con x m x n , ¿cuántas veces terminamos multiplicando “x”? Respuesta: primero “m” veces, luego por otra “n” veces, para un total de “m + n” veces.
Ejemplo: x 2 x 3 = (xx) (xxx) = xxxxx = x 5
Entonces, x 2 x 3 = x (2 + 3) = x 5
La ley que x m / x n = x m-n
Como en el ejemplo anterior, ¿cuántas veces terminamos multiplicando “x”? Respuesta: “m” veces, luego reduce eso por “n” veces (porque estamos dividiendo), para un total de “m-n” veces.
Ejemplo: x 4 / x 2 = (xxxx) / (xx) = xx = x 2
Entonces, x 4 / x 2 = x (4-2) = x 2
(Recuerde que x / x = 1, así que cada vez que ve un x “encima de la línea” y uno “debajo de la línea” usted puede cancelarlos.)
Esta ley también puede mostrarte por qué x 0 = 1 :
Ejemplo: x 2 / x 2 = x 2-2 = x 0 = 1
La ley que (x m ) n = x mn
Primero multiplicas “m” veces. Entonces tienes para hacer eso “n” veces , para un total de m × n veces.
Ejemplo: (x 3 ) 4 = (xxx) 4 = (xxx) (xxx) (xxx) (xxx) = xxxxxxxxxxxx = x 12
Entonces (x 3 ) 4 = x 3 × 4 = x 12
La ley que (xy) n = x n y n
Para mostrar cómo funciona, piense en reorganizar todas las “x” sy “y” s como en este ejemplo:
Ejemplo: (xy) 3 = (xy) (xy) (xy) = xyxyxy = xxxyyy = (xxx) (yyy) = x 3 y 3
La ley que (x / y) n = x n / y n
Similar al ejemplo anterior, simplemente reorganice las “x” sy “y” s
Ejemplo: (x / y) 3 = (x / y) (x / y) (x / y) = (xxx) / (aaa) = x 3 / año 3
La ley que 
OK, ¡este es un poco más complicado!
Le sugiero que lea Exponentes fraccionales primero, o esto puede no tener sentido.
De todos modos, la idea importante es que:
x 1 / n = La n- th Raíz de x
Y así, un exponente fraccional como 4 3/2 realmente dice hacer un cubo (3) y una raíz cuadrada [19459005 ] (1/2), en cualquier orden.
Solo recuerda de las fracciones que m / n = m × (1 / n) :
Ejemplo: 
El orden no importa, por lo que también funciona para m / n = (1 / n) × m :
Ejemplo: 
Exponentes de exponentes …
¿Qué pasa con este ejemplo?
4 3 2
Hacemos el exponente en la parte superior primero , así que lo calculamos de esta manera:
| Comience con: | 4 3 2 | |
| 3 2 = 3 × 3: | 4 9 | |
| 4 9 = 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4 × 4: | 262144 |
¡Y eso es todo!
Si le resulta difícil recordar todas estas reglas, recuerde esto:
puedes resolverlos cuando entiendes el
tres ideas cerca de la parte superior de esta página
Oh, una cosa más … ¿Qué pasa si x = 0?
| Exponente positivo (n> 0) | 0 n = 0 | |
| Exponente negativo (n <0) | 0 -n es indefinido (porque dividiendo por 0 no está definido) | |
| Exponente = 0 | 0 0 … ummm … ¡mira abajo! |
El extraño caso de 0 0
Existen diferentes argumentos para el valor correcto de 0 0
0 0 podría ser 1, o posiblemente 0, por lo que algunas personas dicen que es realmente “indeterminado”:
| |
x 0 = 1, así que … | 0 0 = 1 |
| 0 n = 0, entonces … | 0 0 = 0 | |
| En caso de duda … | 0 0 = “indeterminado” |
Difícil:
