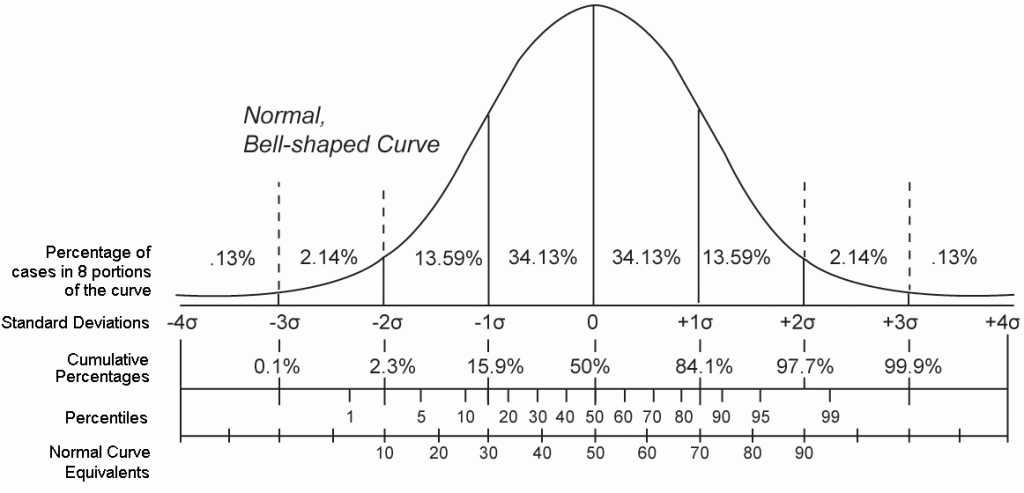
Percentiles
Percentil:
el valor por debajo del cual cae un porcentaje de datos.
Ejemplo:
Eres la cuarta persona más alta en un grupo de 20
El 80% de las personas son más bajas que tú:

Eso significa que estás en el percentil 80 .
Si su altura es de 1.85 m, entonces “1.85 m” es la altura del percentil 80 en ese grupo.
En orden
Tenga los datos en orden , para que sepa qué valores están arriba y abajo.
- Para calcular los percentiles de altura: tenga los datos en orden de altura (ordenados por altura).
- Para calcular los percentiles de edad: tenga los datos en orden de edad.
- Y así sucesivamente.
Datos agrupados
Cuando se agrupan los datos:
Sume todos los porcentajes debajo de el puntaje,
más la mitad el porcentaje en el puntaje.
Ejemplo: ¡Obtienes una B!
En la prueba, el 12% obtuvo D, el 50% obtuvo C, el 30% obtuvo B y el 8% obtuvo A

Obtuviste una B, así que suma
- todo el 12% que obtuvo D,
- todo el 50% que obtuvo C,
- la mitad del 30% que obtuvo B,
para un percentil total de 12% + 50% + 15% = 77%
En otras palabras, lo hiciste “tan bien o mejor que el 77% de la clase”
(¿Por qué tomar la mitad de B? Porque no debes imaginar que obtuviste la “Mejor B” o la “Peor B”, solo un promedio de B.)
Deciles
Los deciles son similares a los percentiles (suenan como decimales y percentiles juntos), ya que dividen los datos en 10% grupos :
- El 1er decil es el 10 ° percentil (el valor que divide los datos de modo que 10% está debajo de él)
- El 2do decil es el vigésimo percentil (el valor que divide los datos así que 20% está debajo de él)
- etc.
Ejemplo: (continuación)

Estás en el octavo decil (el percentil 80).
Cuartiles
Otra idea relacionada es Cuartiles , que divide los datos en cuartos:
Ejemplo: 1, 3, 3, 4, 5, 6, 6, 7, 8, 8
Los números están en orden. Cortar la lista en cuartos:

En este caso, el cuartil 2 está a medio camino entre 5 y 6:
Q2 = (5 + 6) / 2 = 5.5
Y el resultado es:
- Cuartil 1 (Q1) = 3
- Cuartil 2 (Q2) = 5.5
- Cuartil 3 (Q3) = 7
Los cuartiles también dividen los datos en divisiones
del 25%, entonces:
- Cuartil
1 (Q1) se puede llamar el percentil 25 - Cuartil
2 (Q2) se puede llamar el percentil 50 - Cuartil
3 (Q3) se puede llamar el percentil 75
Ejemplo: (continuación)
Para 1, 3, 3, 4, 5, 6, 6, 7, 8, 8 :
- El percentil 25 = 3
- El percentil 50 = 5.5
- El percentil 75 = 7
Estimación de percentiles
Podemos estimar percentiles a partir de un gráfico lineal .

Ejemplo: Compras
Un total de 10,000 personas visitaron el centro comercial durante 12 horas:
| Tiempo (horas) | Gente |
|---|---|
| 0 | 0 |
| 2 | 350 |
| 4 | 1100 |
| 6 | 2400 |
| 8 | 6500 |
| 10 | 8850 |
| 12 | 10,000 |
a) Estimación
el percentil 30 (cuando había llegado el 30% de los visitantes).
b) Estimación
qué percentil de visitantes tenía
llegó después de 11 horas.
Primer sorteo
un gráfico lineal de los datos: trazar los puntos
y unirlos con una curva suave:

a) El 30
El percentil ocurre cuando las visitas alcanzan los 3.000.
Dibuja una línea
horizontalmente a través de 3.000 hasta llegar a la curva, luego dibuja un
línea verticalmente hacia abajo para leer la hora en el eje horizontal:

Entonces el 30
el percentil ocurre después de aproximadamente 6.5 horas .
b) Para estimar
el percentil de visitas después de las 11
horas: dibuja una línea verticalmente hacia arriba desde 11 hasta llegar a la curva, luego
dibuje una línea horizontal para leer la población en la vertical
eje:

Entonces las visitas
en 11 horas fueron alrededor de 9,500, que es el percentil 95 .
