Productos binomiales especiales
Mira lo que sucede cuando multiplicamos algunos binomios …
Binomial
Un binomio es un polinomio con dos términos
 |
| ejemplo de un binomio |
Producto
Producto significa el resultado que obtenemos después de multiplicar.
En álgebra xy significa x multiplicado por y
Y (a + b) (a − b) significa (a + b) multiplicado por (a − b) [19459024 ] ¡Usamos eso mucho aquí!
Productos binomiales especiales
Entonces, cuando multiplicamos binomios, obtenemos … ¡Productos binomiales!
Y veremos tres casos especiales de binomios multiplicadores … así que son Productos binomiales especiales .
1. Multiplicar un binomio por sí mismo
¿Qué sucede cuando cuadramos un binomio (en otras palabras, lo multiplicamos por sí mismo) …?
(a + b) 2 = (a + b) (a + b) = …?
El resultado:
(a + b) 2 = a 2 + 2ab + b 2
Esta ilustración muestra por qué funciona:

2. Restar tiempos Restar
¿Y qué sucede cuando cuadramos un binomio con un menos dentro?
(a − b) 2 = (a − b) (a − b) = …?
El resultado:
(a − b) 2 = a 2 – 2ab + b 2
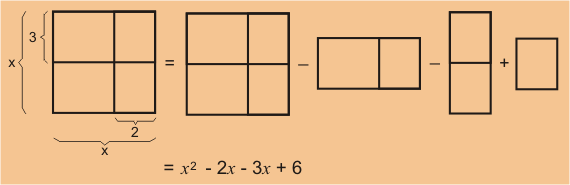
Si quieres ver por qué, observa cómo el cuadrado (a − b) 2 es igual al cuadrado grande a 2 menos los otros rectángulos:

(a − b) 2 = a 2 – 2b (a − b) – b 2
= a 2 – 2ab + 2b 2 – b 2
= a 2 – 2ab + b 2
3. Sumar tiempos Restar
Y luego hay un caso especial más … ¿qué pasa con (a + b) veces (a − b)?
(a + b) (a − b) = …?
El resultado:
(a + b) (a − b) = a 2 – b 2
¡Eso fue interesante! Terminó muy simple.
Y se llama “ diferencia de dos cuadrados ” (los dos cuadrados son a 2 y b 2 [19459028 ] ).
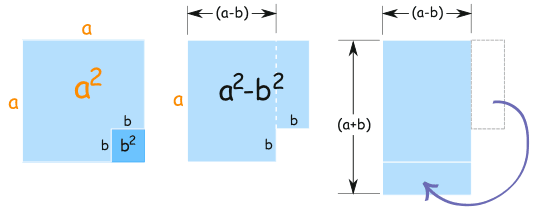
Esta ilustración muestra por qué funciona:
 |
|
a 2 – b 2 es igual a (a + b) (a − b)
[19459019 ] |
Nota: (a − b) podría ser el primero y (a + b) segundo:
(a − b) (a + b) = a 2 – b 2
Los tres casos
Aquí están los tres resultados que acabamos de obtener:
| (a + b) 2 | = a 2 + 2ab + b 2 | } | los “trinomios cuadrados perfectos” |
| (a − b) 2 | = a 2 – 2ab + b 2 | ||
| (a + b) (a − b) | = a 2 – b 2 | la “diferencia de cuadrados” |
Recuerda esos patrones, te ahorrarán tiempo y te ayudarán a resolver muchos acertijos de álgebra.
Utilizándolos
Hasta ahora hemos usado “a” y “b”, pero podrían ser cualquier cosa.
Ejemplo: (y + 1) 2
Podemos usar el caso (a + b) 2 donde “a” es y, y “b” es 1:
(y + 1) 2 = (y) 2 + 2 (y) (1) + (1) 2 = y 2 + 2y + 1
Ejemplo: (3x − 4) 2
Podemos usar el caso (a-b) 2 donde “a” es 3x y “b” es 4:
(3x − 4) 2 = (3x) 2 – 2 (3x) (4) + (4) 2 = 9x 2 – 24x + 16
Ejemplo: (4y + 2) (4y − 2)
Sabemos que el resultado es la diferencia de dos cuadrados, porque:
(a + b) (a − b) = a 2 – b 2
entonces:
(4y + 2) (4y − 2) = (4y) 2 – (2) 2 = 16y 2 – 4 [ 19459038]
A veces podemos ver el patrón de la respuesta:
Ejemplo: qué binomios se multiplican para obtener 4x 2 – 9
Hmmm … ¿es esa la diferencia de dos cuadrados?
¡Sí!
4x 2 es (2x) 2 , y 9 es (3) 2 , entonces tenemos:
4x 2 – 9 = (2x) 2 – (3) 2
Y eso puede ser producido por la fórmula de la diferencia de cuadrados:
(a + b) (a − b) = a 2 – b 2
Así (“a” es 2x y “b” es 3):
(2x + 3) (2x − 3) = (2x) 2 – (3) 2 = 4x 2 – 9
Entonces la respuesta es que podemos multiplicar (2x + 3) y (2x − 3) para obtener 4x 2 – 9 [ 19459024]
