Racionalizar el denominador
 |
“Racionalizar el denominador” es cuando movemos una raíz (como una raíz cuadrada o raíz cúbica ) desde la parte inferior de una fracción hacia la parte superior . |
¡Oh, no! Un denominador irracional!
El fondo de una fracción se llama denominador .
Los números como 2 y 3 son racionales .
Pero muchas raíces, como √2 y √3, son irracionales .
Ejemplo: 
tiene un denominador irracional
tiene un denominador irracional 
Para estar en “forma más simple”, el denominador no debería ser irracional.
Arreglando (haciendo racional el denominador)
se llama “ Racionalizar el denominador ”
Nota: no hay nada incorrecto con un denominador irracional, todavía funciona. Pero no es la “forma más simple”, por lo que puede costarle marcas .
Y eliminarlos puede ayudarlo a resolver una ecuación, por lo que debe aprender cómo hacerlo.
Entonces … ¿cómo lo hacemos?
1. Multiplicar tanto la parte superior como la inferior por una raíz
A veces podemos simplemente multiplicar la parte superior e inferior por una raíz:
Ejemplo: tiene un denominador irracional. Vamos a arreglarlo
Multiplica arriba y abajo por la raíz cuadrada de 2, porque: √2 × √2 = 2:
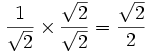
Ahora el denominador tiene un número racional (= 2). ¡Hecho!
Nota: está bien tener un número irracional en la parte superior (numerador) de una fracción.
2. Multiplicar tanto la parte superior como la inferior por el conjugado
Hay otra forma especial de mover una raíz cuadrada desde la parte inferior de una fracción hacia la parte superior … multiplicamos tanto la parte superior como la parte inferior por el conjugado de el denominador .
El conjugado es donde nosotros cambiamos el signo en el medio de dos términos:
| Ejemplo de expresión | Su conjugado | |
|---|---|---|
| x 2 – 3 | x 2 + 3 |
| Otro ejemplo | Su conjugado | |
|---|---|---|
| a + b 3 | a – b 3 |
Funciona porque cuando multiplicamos algo por su conjugado obtenemos cuadrados así:
(a + b) (a − b) = a 2 – b 2
Aquí es cómo hacerlo:
Ejemplo: aquí hay una fracción con un “denominador irracional”:
1
3 − √2
1
3 − √2
¿Cómo podemos mover la raíz cuadrada de 2 a la parte superior?
Podemos multiplicar arriba y abajo por 3 + √2 (el conjugado de 3 − √2) , que no cambiará el valor de la fracción: [19459024 ]
1
3 − √2
×
3 + √2
3 + √2
=
3 + √2
3 2 – (√2) 2
=
3 + √2
7
(¿Viste que usamos (a + b) (a − b) = a 2 – b 2 en el denominador?) [ 19459024]
Usa tu calculadora para calcular el valor antes y después … ¿es lo mismo?
Hay otro ejemplo en la página Evaluación de límites (tema avanzado) donde muevo una raíz cuadrada de arriba hacia abajo.
Útil
Así que intenta recordar estos pequeños trucos, ¡puede que te ayuden a resolver una ecuación algún día!