¡Regla de los primeros dígitos!
(Ley de Benford)
No hagas trampa con los números,
Pueden regalarte.
Eso dice Ley de Benford.
Primeros dígitos
¿Con qué frecuencia esperaría que un “1” sea el primer dígito en un conjunto de números?
Ejemplo: está viendo una lista de gastos, con números como:
- $ 65.20 (el primer dígito es 6 )
- $ 35.00 (el primer dígito es 3 )
- $ 7.50 (el primer dígito es 7 )
- $ 12.50 (el primer dígito es 1 )
¿Habría tantos 1 como 2 ‘s para el primer dígito?
Bueno 1 es solo un número como 2 a 9 , ¿Correcto?
Entonces parece que debería ser el primer dígito 1 de cada 9 veces (aproximadamente el 11%) :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 11% | 11% | 11% | 11% | 11% | 11% | 11% | 11% | 11% |
¡Pero no!
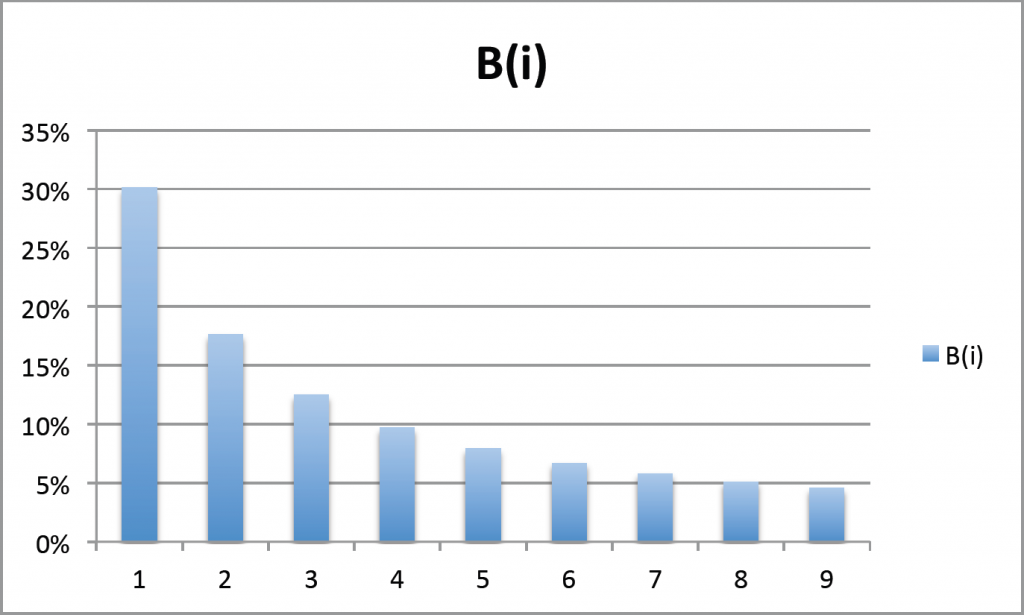
Un hombre llamado Dr. Frank Benford descubrió que en muchos casos, el número 1 es el primer dígito aproximadamente el 30% del tiempo .
Y el pobre número antiguo 9 es el primer dígito solo el 5% del tiempo.

La historia es que un hombre llamado Simon Newcomb notó que un libro de logaritmos estaba muy desgastado al principio pero no al final.
“¿Por qué la gente está más interesada en 1’s y 2’s que 8’s y 9’s?”
¡Decidió investigar! (¿Investigarías algo extraño?)
El Dr. Benford descubrió que esto sorprendente también sucedió con las estadísticas de béisbol, áreas de ríos, tamaños de población, direcciones de calles y muchos más casos.
¿Por qué es esto?
Bueno, pensemos en las direcciones de las calles:
¿Cuáles son los primeros dígitos de los números de casa?
- algunas calles son cortas: 1,2,3,4,5,6
- algunas calles son más largas: 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 (observe cuántas, tenga 1 como primer dígito ?)
- otras calles son un poco más largas, con números del 1 al 30 (muchos “1” y “2” s)
- Y cuando las calles son muy largas, tenemos muchas a partir de 100.
El resultado es que los números que comienzan con 1 son más comunes, 2 también es bastante común y 9 menos.
Ejemplo: Precios de acciones
Digamos que un precio comienza en 1.00 y sube un 10% cada vez:
| Precio | Primer dígito |
|---|---|
| 1,00 | 1 |
| 1.10 | 1 |
| 1.21 | 1 |
| 1.33 | 1 |
| 1,46 | 1 |
| 1.61 | 1 |
| 1.77 | 1 |
| 1,95 | 1 |
| 2.14 | 2 |
| 2,36 | 2 |
| 2.59 | 2 |
| 2,85 | 2 |
| 3.14 | 3 |
| 3.45 | 3 |
| 3,80 | 3 |
| 4.18 | 4 |
| 4,59 | 4 |
| 5.05 | 5 |
| 5,56 | 5 |
| 6.12 | 6 |
| 6,73 | 6 |
| 7.40 | 7 |
| 8,14 | 8 |
| 8,95 | 8 |
| 9.85 | 9 |
Muchos 1 ‘s, bastantes 2 ‘ s, menos 3 ‘s, etc.
El resultado
De hecho, Benford calculó que la probabilidad de que un primer dígito sea d es:
P (d) = log 10 (1 + 1 / d)
Ejemplo: la probabilidad de un primer dígito de 2:
Y estas son las probabilidades:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 30,1% | 17,6% | 12,5% | 9,7% | 7,9% | 6,7% | 5,8% | 5,1% | 4,6% |
Ejemplo: Sam revisó una lista de 100 gastos de trabajo para el año.
Había $ 1.95 por un bolígrafo, $ 4.95 por un marcador, etc. Aquí están los recuentos de los primeros dígitos :
| Primer dígito: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Cuenta: | 26 | 19 | 10 | 11 | 9 | 15 | 2 | 5 | 4 |
Sigue la Ley de Benford bastante bien.
Excepto que hay muchos “6”, porque el papel de la impresora cuesta $ 6 y compran mucho.
Loterías

Los números de la lotería no siguen esta regla, porque no son el tamaño o la cantidad de nada, en realidad son solo símbolos (y una lotería funcionaría igual usando letras o imágenes).
Encontrar tramposos

Cuando las personas intentan falsificar números, a menudo eligen el primer dígito al azar y terminan con tantos “9” como “1” s.
Pero un programa de computadora puede revisar todos los números y contar los primeros dígitos para ver con qué frecuencia aparece un “1” en comparación con un “5” o “9”. Si parece sospechoso … ¡cuidado!
Esto puede ayudar a descubrir trampas fiscales, fraude electoral y más.
Tu turno
Reúna una lista de 100 números de una categoría de su elección. Asegúrese de que los números cuentan o miden algo (y no son solo símbolos).
Aquí hay algunas sugerencias:
- Números de casa
- Poblaciones de la ciudad
- Precios de supermercado
- Precios de automóviles usados
Encuentra sus primeros dígitos y completa esta tabla:
| Primer dígito: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Cuenta: |
¿Qué encontraste?
Actividad de bonificación
Haz que algunos amigos hagan listas de compras simuladas con cuánto cuesta cada artículo. Encuentre los primeros dígitos y póngalos en una tabla:
| Primer dígito: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Cuenta: |
¿Qué encontraste?
