Tabla de distribución normal estándar

Esta es la curva “en forma de campana” de la distribución normal estándar.
Es una Distribución normal con media 0 y desviación estándar 1.

 

Te muestra el porcentaje de población:

  • entre 0 y Z (opción “0 a Z”)
  • menor que Z (opción “Hasta Z”)
  • mayor que Z (opción “Z en adelante”)

Solo muestra valores al 0.01%

 

La ​​mesa

También puede usar la tabla a continuación. La tabla muestra el área de 0 a Z.

En lugar de una tabla LARGA, hemos puesto “ 0.1 ” en ejecución, luego “” 0.01 en ejecución. (A continuación se muestra un ejemplo de cómo usarlo)

Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0.1103 0.1141
0,3 0.1179 0,1217 0,1255 0,1293 0.1331 0,1368 0,1406 0.1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0.1808 0,1844 0,1879
0,5 0,1915 0,1950 0.1985 0,2019 0,2054 0,2088 0.2123 0.2157 0.2190 0.2224
0,6 0.2257 0.2291 0.2324 0.2357 0,2389 0,2422 0.2454 0.2486 0.2517 0.2549
0,7 0.2580 0,2611 0.2642 0.2673 0,2704 0,2734 0,2764 0.2794 0.2823 0.2852
0,8 0.2881 0.2910 0.2939 0.2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133
0,9 0,3159 0,3186 0,3212 0,3238 0,3264 0.3289 0,3315 0,3340 0,3365 0.3389
1,0 0,3413 0,3438 0.3461 0,3485 0,3508 0,3531 0.3554 0.3577 0,3599 0.3621
1.1 0.3643 0,3665 0.3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
1.2 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015
1.3 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177
1.4 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319
1,5 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,44441
1,6 0,4452 0,44463 0.4474 0,4484 0.4495 0,4505 0,4515 0,4525 0,4535 0,4545
1,7 0,4554 0,4564 0,4573 0.4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633
1,8 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706
1,9 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767
2,0 0,4772 0,4778 0.4783 0,4788 0,4793 0,4798 0,4803 0,4808 0,4812 0,4817
2.1 0,4821 0,4826 0,4830 0,4834 0,4838 0,4842 0,4846 0,4850 0,4854 0,4857
2.2 0,4861 0,4864 0,4868 0,4871 0,4875 0,4878 0.4881 0.4884 0.4887 0,4890
2,3 0.4893 0.4896 0,4898 0,4901 0,4904 0,4906 0,4909 0,4911 0,4913 0,4916
2.4 0,4918 0,4920 0,4922 0,4925 0,4927 0,4929 0,4931 0,4932 0,4934 0,4936
2,5 0,4938 0,4940 0,4941 0,4943 0,4945 0,4946 0,4948 0,4949 0,4951 0,4952
2,6 0,4953 0,4955 0,4956 0,4957 0,4959 0,4960 0,4961 0,4962 0,4963 0,4964
2.7 0,4965 0,4966 0,4967 0,4968 0,4969 0,4970 0,4971 0,4972 0,4973 0,4974
2,8 0,4974 0,4975 0,4976 0,4977 0,4977 0,4978 0,4979 0,4979 0,4980 0,4981
2,9 0,4981 0,4982 0,4982 0.4983 0,4984 0,4984 0.4985 0.4985 0.4986 0.4986
3,0 0.4987 0.4987 0.4987 0,4988 0,4988 0,4989 0,4989 0,4989 0,4990 0,4990

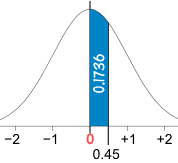
Ejemplo: porcentaje de población entre 0 y 0,45

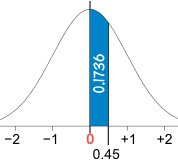
standard normal distribution 0.45 = 0.1736

Comienza en la fila de 0.4 y sigue leyendo
hasta 0,45: existe el valor 0,1736

Y 0.1736 es 17.36%

Entonces el 17,36% de la población tiene entre 0 y 0,45 desviaciones estándar de la media.

Debido a que la curva es simétrica, se puede usar la misma tabla para valores que van en cualquier dirección, por lo que es negativo
0.45 también tiene un área de 0.1736

Ejemplo: porcentaje de población Z entre -1 y 2

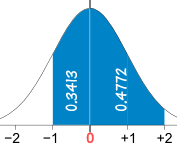
standard normal distribution -1 to +2

De −1 a 0 es lo mismo que de 0 a +1 :

En la fila de 1.0, primera columna 1.00, está el valor 0.3413

De 0 a +2 es:

En la fila para 2.0, primera columna 2.00, está el valor 0.4772

Suma los dos para obtener el total entre -1 y 2:

0.3413 + 0.4772 = 0.8185

Y 0.8185 es 81.85%

Entonces el 81.85% de la población tiene entre -1 y +2 desviaciones estándar de la media.

  Distribución normal
  Desviación estándar
  Quincunx Menú de probabilidad y estadísticas