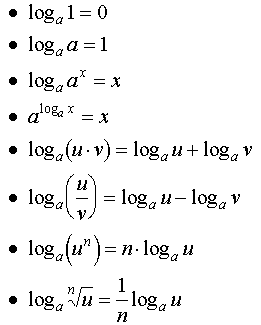
Trabajando con exponentes y logaritmos
¿Qué es un exponente?
 |
El exponente de un número dice cuántas veces
En este ejemplo: 2 3 = 2 × 2 × 2 = 8
(2 se usa 3 veces en una multiplicación para obtener 8) |
¿Qué es un logaritmo?
A Logaritmo va a la inversa.
Hace la pregunta “¿qué exponente produjo esto?”:
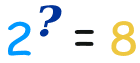
Y lo responde así:
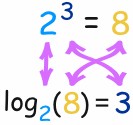
En ese ejemplo:
- El exponente toma 2 y 3 y da 8 (2, usado 3 veces en una multiplicación, hace 8)
- El Logaritmo toma 2 y 8 y da 3 (2 hace 8 cuando se usa 3 veces en una multiplicación)
Un logaritmo dice cuántos de un número se multiplican para obtener otro número
Entonces, un logaritmo realmente te da el exponente como respuesta :
(Vea también cómo Exponentes, raíces y logaritmos están relacionados.)
Trabajando juntos
Los exponentes y los logaritmos funcionan bien juntos porque se “deshacen” entre sí (siempre que la base “a” sea la misma):
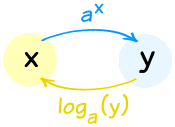
Son ” Funciones inversas ”
Hacer uno, luego el otro, te lleva de vuelta a donde empezaste:
Es una pena que estén escritos de manera tan diferente … hace que las cosas se vean extrañas. Por lo tanto, puede ayudar pensar en a x como “arriba” y log a (x) como “abajo”: [19459017 ]
De todos modos, lo importante es que:
La función exponencial “deshace” la función logarítmica.
(y viceversa)
Como en este ejemplo:
Ejemplo, qué es x en log 3 (x) = 5
Queremos “deshacer” el registro 3 para que podamos obtener “x =”
, entonces: x = 3 5
Y también:
Ejemplo: Calcular y en y = log 4 (1/4)
Ahora un truco simple: 1/4 = 4 −1
Propiedades de logaritmos
Una de las cosas poderosas sobre los logaritmos es que pueden convertirse en multiplicar en sumar .
log a (m × n) = log a m + log a n
“el registro de multiplicación es la suma de los registros”
¿Por qué es eso cierto? Ver Nota al pie .
Usando esa propiedad y las Leyes de exponentes obtenemos estas propiedades útiles:
| log a (m × n) = log a m + log a n | el registro de multiplicación es la suma de los registros |
| log a (m / n) = log a m – log a n | el registro de división es la diferencia de los registros |
| log a (1 / n) = −log a n | esto solo sigue a la regla de “división” anterior, porque log a (1) = 0 |
| log a (m r ) = r (log a m ) | el logaritmo de m con un exponente r es r veces el logaritmo de m |
Recuerde: ¡la base “a” es siempre la misma!
Historia: Los logaritmos eran muy útiles antes de que se inventaran las calculadoras … por ejemplo, en lugar de multiplicar dos números grandes, usando logaritmos podría convertirlo en suma (¡mucho más fácil!) [ 19459017]
Y había libros llenos de tablas de Logaritmo para ayudar.
Divirtámonos usando las propiedades:
Ejemplo: Simplificar log a ((x 2 +1) 4 √x)
Eso es todo lo que podemos simplificar … no podemos hacer nada con log a (x 2 +1) .
Respuesta: 4 log a (x 2 +1) + ½ log a (x)
Nota: no existe una regla para manejar log a (m + n) o log a (m − n)
También podemos aplicar las reglas de logaritmo “hacia atrás” para combinar logaritmos:
Ejemplo: Convierta esto en un logaritmo: log a (5) + log a (x) – log a (2)
Respuesta: log a (5x / 2)
El logaritmo natural y las funciones exponenciales naturales
Cuando la base es e (” Número de Euler ” = 2.718281828459 …) obtenemos:
- El logaritmo natural log e (x) que se escribe más comúnmente ln (x)
- La función exponencial natural e x
Y la misma idea de que uno puede “deshacer” al otro sigue siendo cierta:
ln (e x ) = x
e (ln x) = x
Y aquí están sus gráficos:
|
Logaritmo natural |
Función exponencial natural |
|
 |
 |
|
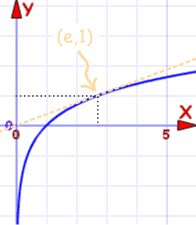
| Gráfico de f (x) = ln (x) |
Gráfico de f (x) = e x
|
|
|
Pases a través de (1,0) y (e, 1) |
Pases a través de (0,1) y (1, e) |
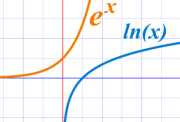
Son la misma curva con el eje xy el eje y volteados .
Que es otra cosa para mostrarle que son funciones inversas.
 |
En una calculadora, el logaritmo natural es el botón “ln”. |
Siempre intenta usar logaritmos naturales y la función exponencial natural siempre que sea posible.
El logaritmo común
Cuando la base es 10 obtienes:
- El logaritmo común log 10 (x) , que a veces se escribe como log (x)
A los ingenieros les encanta usarlo, pero no se usa mucho en matemáticas.
 |
En una calculadora, el logaritmo común es el botón “log”.
Es útil porque te dice qué tan “grande” es el número en decimal (cuántas veces necesitas usar 10 en una multiplicación). |
Ejemplo: Calcular log 10 100
Bueno, 10 × 10 = 100, entonces cuando se usa 10 2 veces en una multiplicación obtienes 100:
log 10 100 = 2
Del mismo modo log 10 1,000 = 3, log 10 10,000 = 4, y así sucesivamente.
Ejemplo: Calcular log 10 369
OK, es mejor usar el botón “log” de mi calculadora:
log 10 369 = 2.567 …
Cambio de la base
¿Qué pasa si queremos cambiar la base de un logaritmo?
¡Fácil! Solo usa esta fórmula:
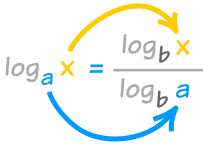
“x sube, a baja”
O otra forma de pensarlo es que log b a es como un “factor de conversión” (misma fórmula que arriba):
log a x = log b x / log b a
Entonces ahora podemos convertir de cualquier base a cualquier otra base.
Otra propiedad útil es:
log a x = 1 / log x a
¿Ves cómo “x” y “a” intercambian posiciones?
Ejemplo: Calcular 1 / log 8 2
1 / log 8 2 = log 2 8
Y 2 × 2 × 2 = 8, entonces cuando se usa 2 3 veces en una multiplicación obtienes 8:
1 / log 8 2 = log 2 8 = 3
Pero usamos el logaritmo natural con más frecuencia, por lo que vale la pena recordarlo:
log a x = ln x / ln a
Ejemplo: Calcular log 4 22
| |
Mi calculadora no tiene un botón “ log 4 ” …
… pero tiene un botón “ ln “, por lo que podemos usar eso: |
¿Qué significa esta respuesta? Significa que 4 con un exponente de 2.23 es igual a 22. Entonces podemos verificar esa respuesta:
Verificación: 4 2.23 = 22.01 (¡lo suficientemente cerca!)
Aquí hay otro ejemplo:
Ejemplo: Calcular log 5 125
Sé que 5 × 5 × 5 = 125, (5 se usa 3 veces para obtener 125), así que esperaba una respuesta de 3 , y funcionó !
Uso en el mundo real
Estos son algunos usos de los logaritmos en el mundo real:
Terremotos
La magnitud de un terremoto es una escala logarítmica.
La famosa “Escala de Richter” utiliza esta fórmula:
M = log 10 A + B
Donde A es la amplitud (en mm) medida por el sismógrafo
y B es un factor de corrección de distancia
Hoy en día hay fórmulas más complicadas, pero aún usan una escala logarítmica.
Sonido
El volumen se mide en decibelios (dB para abreviar):
Volumen en dB = 10 log 10 (p × 10 12 )
donde p es la presión acústica.
Ácido o alcalino
La acidez (o alcalinidad) se mide en pH:
pH = −log 10 [H + ]
donde H + es la concentración molar de iones de hidrógeno disueltos.
Nota: en química [] significa concentración molar (moles por litro).
Más ejemplos
Ejemplo: resolver 2 log 8 x = log 8 16
Pero … pero … pero … ¡no puedes tener un registro de un número negativo!
Entonces el caso −4 no está definido.
Respuesta: 4
Comprueba: usa tu calculadora para ver si esta es la respuesta correcta … también prueba el caso “−4”.
Ejemplo: Resolver e – w = e 2w + 6
]
Respuesta: w = – 2
Verificación: e – (- 2) = e 2 y e 2 (−2) +6 = e 2
Nota al pie: ¿Por qué log (m × n) = log (m) + log (n) ?
Para ver por qué , utilizaremos y :
| Primero, convierta m y n en “exponentes de logaritmos”: | |
 |
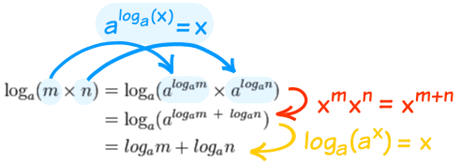Luego usa una de las Leyes de exponentes Finalmente deshacer los exponentes. |
Es una de esas cosas inteligentes que hacemos en matemáticas que puede describirse como “no podemos hacerlo aquí, así que vamos allí , luego hagámoslo, luego volvemos “